Eine freie Initiative von Menschen bei mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| Use Google Translate for a raw translation of our pages into more than 100 languages. Please note that some mistranslations can occur due to machine translation. |
Bachminze (Mentha aquatica)
Wasserminze
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||
| Mentha aquatica | ||||||||||||
| L. |
Die Wasserminze (Mentha aquatica), auch Bachminze genannt[1], ist eine Pflanzenart in der Familie der Lippenblütler (Lamiaceae). Sie kommt in weiten Gebieten Europas vor.
Beschreibung

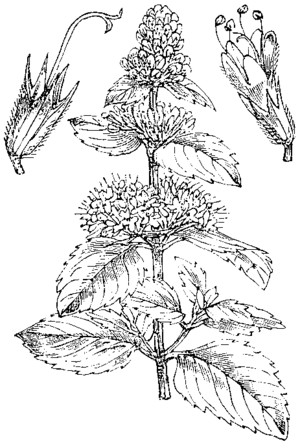



Erscheinungsbild und Laubblatt
Die Wasserminze wächst als ausdauernde krautige Pflanze, die Wuchshöhen von meist 20 bis 50 (10 bis 100) Zentimeter erreicht. An Land werden unterirdische und im Wasser auch oberirdische Ausläufer gebildet. Der aufrechte und meist verzweigte Stängel ist vierkantig.
Die gegenständig am Stängel angeordneten Laubblätter sind lang gestielt. Die einfache Blattspreite ist eiförmig elliptisch, etwas derb und oft glänzend, mit gesägtem Blattrand. Es sind vier bis sechs Paare bogiger Fiedernerven vorhanden. Besonders die Blätter riechen beim Zerreiben nach Pfefferminz.
Blütenstand, Blüte und Frucht
Die Blüten stehen dicht in den Achseln der oberen Blätter in stehenden, locker übereinander angeordneten Scheinquirlen und in einem endständigen kugeligen, kopfigen Teilblütenstand zusammen.
Die Blüten sind zygomorph und fünfzählig mit doppelter Blütenhülle. Die fünf nur etwas ungleichen Kelchblätter sind teilweise röhrig verwachsen mit 13 Nerven und fünf lanzettlichen Kelchzähnen. Die fünf hellvioletten, rosafarbenen, fleischigrosafarbenen bis weißen Kronblätter sind unterschiedlich stark verwachsen und nur schwach zweilippig. Die Oberlippe ist meist so groß wie einer der drei Lappen der Unterlippe. Hierdurch scheint die Blüte fast regelmäßig vierspaltig. Von den vier geraden, fertilen Staubblättern sind zwei etwas länger.
Die Klausenfrüchte zerfallen in vier oben warzige Teilfrüchte.
Chromosomenzahl
Die Chromosomenzahl beträgt 2n = 96.
Ökologie
Die Wasserminze ist ein Hemikryptophyt (Schaftpflanze) bzw. eine Sumpfpflanze und ein Ausläufer-Kriechpionier. Die Blätter enthalten reichlich ätherische Öle.
Die Blüten sind unscheinbare „Kleine Trichterblumen“. Der Nektar wird am Grunde der Blüte von einer großen Nektardrüse abgesondert und durch lange Innenhaare der Blütenkrone („Saftdecke“) geschützt. Die Pflanze ist meist unvollständig zweihäusig (gynodiözisch), d. h. neben zwittrigen Pflanzen gibt es auch weibliche mit kleineren Blüten (so bei wie bei allen Arten der Gattung Minzen). Die Blüten duften und werden deshalb intensiv von verschiedenen Insekten, beispielsweise Bienen, Schwebfliegen und vielen anderen Arten besucht.
Die Ausbreitung der Samen erfolgt über das Wasser (Hydrochorie).
Vegetative Vermehrung erfolgt, wie bei allen Minzen-Arten durch ober- und unterirdische Ausläufer.
Vorkommen
Wasserminze ist in großen Teilen Europas und Afrikas zu finden. Des Weiteren ist sie auch in Makaronesien, auf Zypern, im Libanon, in Israel, in Palästina, der Türkei, im Kaukasus und im Iran verbreitet.[2][3]
Die Wasserminze gedeiht bei uns häufig in Röhricht- und Großseggen-Gesellschaften, an Ufern und Gräben, in Nass- und Moorwiesen, in Bruchwäldern und im Weidengebüsch. Bevorzugt wächst sie in etwas saurem, schlammigem Boden. Nach Ellenberg ist sie eine Halblichtpflanze, ein Mäßigwärmezeiger, ein Nässezeiger, ein Schwachsäure- bis Schwachbasezeiger. Sie wächst auf mäßig stickstoffreichen Standorten. Sie ist nach Oberdorfer eine Ordnungsscharakterart der Stillwasser-Röhrichte im Süßwasser (Phragmitetalia). Sie kommt aber auch in Gesellschaften der Verbände Filipendulion, Alnion oder Salicion cinereae vor. In den Allgäuer Alpen steigt sie kaum bis zu einer Höhenlage von 1000 Metern auf.[4]
Geschichte als Arzneipflanze
Die Wasserminze zählte neben dem Echten Mädesüß (Filipendula ulmaria) und dem Eisenkraut (Verbena officinalis) zu den heiligen Kräutern der Druiden. In Mittelalter und früher Neuzeit noch wurde die Wasserminze unter anderem gegen das „Seitenstechen“ eingesetzt. Bereits im 16. Jahrhundert taucht auch der botanische Name Menta aquatica bei Eucharius Rößlin auf.[5]
Systematik
Die Erstveröffentlichung von Mentha aquatica erfolgte 1753 durch Carl von Linné in Species Plantarum, 2, S. 576. Synonyme für Mentha aquatica L. sind unter vielen anderen Mentha acuta Opiz, Mentha acutata Opiz, Mentha acuta Strail, Mentha hirsuta Huds., Mentha palustris Mill., Mentha dumetorum var. natalensis Briq., Mentha braunii Oborný, Mentha capitata Opiz, Mentha ortmanniana Opiz, Mentha riparia Schreb., Mentha aquatica subsp. caput-medusae Trautm. & Urum., Mentha aquatica subsp. ortmanniana (Opiz) Lemke.[6]
Man kann zwei Unterarten unterscheiden:
- Mentha aquatica L. subsp. aquatica
- Mentha aquatica subsp. litoralis Hartm. (Syn.: Mentha litoralis (Hartm.) Neuman)
Aus einer Kreuzung der Wasserminze (Mentha aquatica) mit der Grünen Minze (Mentha spicata) ging 1696 in einem Arzneigarten in England die Hybride Pfefferminze (Mentha × piperita) hervor, die einen angenehmeren Duft und Geschmack hat als ihre Eltern.
Die Quirl-Minze (Mentha × verticillata) ist eine Kreuzung zwischen der Ackerminze (Mentha arvensis) und der Wasserminze. Sie liegt in allen Merkmalen zwischen ihren beiden Eltern, ist oft etwas kräftiger und kann diese dann verdrängen.
Siehe auch
- Wasserminze - Artikel in der deutschen Wikipedia
Literatur
- Johann Christoph Röhling, Franz Carl Mertens & Wilhelm Daniel Joseph Koch: Deutschlands Flora, Band 4, Wilmans, 1833. Google-Books-Online.: Mentha aquatica auf Seite 552.
Weblinks
- Die Verbreitung auf der Nordhalbkugel
- Datenblatt bei Wild Flowers of Ireland.
- Picsearch: Mentha aquatica
- Picsearch: Mentha citrata
Einzelnachweise
- ↑ Hermann Fischer: Mittelalterliche Pflanzenkunde, München 1929 (= Geschichte der Wissenschaften: Geschichte der Botanik, 2), Neudruck, mit einem Vorwort von Johannes Steudel, Hildesheim 1967, S. 275.
- ↑ Jelitto/Schacht/Simon: Die Freilandschmuckstauden, S. 610 ff., Verlag Eugen Ulmer & Co., 5. Auflage 2002. ISBN 3-8001-3265-6
- ↑ Rafaël Govaerts (Hrsg.): Mentha - World Checklist of Selected Plant Families des Royal Botanic Gardens, Kew. Zuletzt eingesehen am 10. Januar 2018.
- ↑ Erhard Dörr, Wolfgang Lippert: Flora des Allgäus und seiner Umgebung. Band 2, Seite 414. IHW-Verlag, Eching bei München, 2004. ISBN 3-930167-61-1
- ↑ Eucharius Rößlin: Der Swangern frawen und hebammen roßgarten, Worms 1513, Neudruck Berlin o. J., O II recto
- ↑ Euro+Med Plantbase Project: Mentha aquatica
| Bitte beachten Sie den Hinweis zu Gesundheitsthemen! |
| Dieser Artikel basiert (teilweise) auf dem Artikel Bachminze (Mentha aquatica) aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons Attribution/Share Alike. In Wikipedia ist eine Liste der Autoren verfügbar. |






