Eine freie Initiative von Menschen bei mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| Use Google Translate for a raw translation of our pages into more than 100 languages. Please note that some mistranslations can occur due to machine translation. |
Logik und Satz von Pascal: Unterschied zwischen den Seiten
imported>Odyssee Keine Bearbeitungszusammenfassung |
imported>Joachim Stiller |
||
| Zeile 1: | Zeile 1: | ||
[[ | [[Datei:Pascal-6points-3-s.svg|250px|mini|Satz von Pascal in der reellen affinen Ebene: Sind zwei Paare gegenüberliegender Seiten parallel, so auch das dritte Paar]] | ||
[[Datei:Pascal-6points-s.svg|250px|mini|Satz von Pascal]] | |||
[[Datei:Pascal-6points-graph-s.svg|150px|mini|Satz von Pascal: Kanten-Graph]] | |||
[[Datei:Pascal-6points-2-s.svg|450px|mini|Satz von Pascal: Indizes 2 und 5 vertauscht]] | |||
Der '''Satz von Pascal''' (nach [[Blaise Pascal]]) ist eine Aussage über ein 6-Eck auf einem nicht ausgearteten Kegelschnitt in einer [[Projektive Ebene|projektiven Ebene]]. Er lässt sich in der reellen affinen Ebene wie folgt formulieren: | |||
: Für ein 6-Eck <math>P_1,P_2,P_3,P_4,P_5,P_6</math> auf einer Ellipse bei dem zwei Paare gegenüberliegender Seiten parallel sind (im Bild <math>\overline{P_1P_2} \parallel \overline{P_4P_5},\;\overline{P_6P_1}\parallel \overline{P_3P_4}</math>), ist auch das dritte Paar gegenüberliegender Seiten parallel (im Bild: <math> \overline{P_2P_3} \parallel \overline{P_5P_6}</math>). | |||
Betrachtet man diesen Satz in dem projektiven Abschluss einer affinen Ebene (man nimmt die "Ferngerade", auf der sich parallele Geraden schneiden, hinzu), so gilt: | |||
== | Für beliebige 6 Punkte <math>P_1,P_2,P_3,P_4,P_5,P_6 </math> eines [[Projektiver Kegelschnitt|nicht ausgearteten Kegelschnitts]] in einer projektiven Ebene liegen die Punkte | ||
: <math> P_7:= \overline{P_1P_2}\cap \overline{P_4P_5},</math> | |||
: <math> P_8:= \overline{P_6P_1}\cap \overline{P_3P_4},</math> | |||
: <math> P_9:= \overline{P_2P_3}\cap \overline{P_5P_6}</math> | |||
auf einer Gerade, der '''Pascal-Gerade''' (s. Bild). | |||
Die ''Nummerierung'' gibt an, welche 6 der 15 Verbindungsgeraden der 6 Punkte benutzt werden und welche Kanten benachbart sind. Die Nummerierung ist so gewählt, dass der Kantengraph durch ein reguläres 6-Eck dargestellt werden kann. Geraden zu gegenüberliegenden Kanten des Kantengraphs werden also geschnitten. Sollen andere Kanten in die Pascalfigur eingehen, muss man die Indizes entsprechend permutieren. Für die 2. Pascal-Konfiguration wurden die Indizes 2 und 5 vertauscht (s. Bild, unten). | |||
''Nichtausgeartet'' heißt hier: keine 3 Punkte liegen auf einer Gerade. Den Kegelschnitt kann man sich also als Ellipse vorstellen. (Ein sich schneidendes Geradenpaar ist ein ''ausgearteter'' Kegelschnitt.) | |||
= | ''Kegelschnitte'' sind nur in solchen projektiven Ebenen definiert, die sich über (kommutativen) [[Körper (Algebra)|Körpern]] koordinatisieren lassen. Beispiele von Körpern sind: die [[reelle Zahl|reellen Zahlen]] <math>\R</math>, die [[rationale Zahl|rationalen Zahlen]] <math>\Q</math>, die [[Komplexe Zahl|komplexen Zahlen]] <math>\Complex</math>, [[Körper (Algebra)#Endliche Körper|endliche Körper]]. Jeder nicht ausgeartete Kegelschnitt einer projektiven Ebene lässt sich in geeigneten [[Homogene Koordinaten|homogenen Koordinaten]] durch die Gleichung <math> x_1x_2=x_0^2</math> beschreiben (s. [[projektiver Kegelschnitt]]). | ||
== Bezug zu anderen Sätzen und Verallgemeinerungen == | |||
[[Datei:Pascal-3456-s.svg|450px|mini|Satz v.Pascal: Ausartungen]] | |||
* Der Satz von Pascal ist die [[Dualität (Mathematik)#Dualitätsprinzip der projektiven Geometrie und in Inzidenzstrukturen|duale]] Version des [[Satz von Brianchon|Satzes von Brianchon]]. | |||
* Zum Satz von Pascal gibt es ''Ausartungen'' mit 5 bzw. 4 bzw. 3 Punkten (auf einem Kegelschnitt). Bei einer Ausartung fallen zwei durch eine Kante verbundene Punkte formal zusammen und die zugehörige Sekante der Pascalfigur wird durch die Tangente in dem verbleibenden Punkt ersetzt. Siehe hierzu die Figur und weblink ''planar circlegeometries'', S. 30–35. Durch eine geeignete Wahl einer Gerade der Pascalfiguren als Ferngerade ergeben sich Schließungssätze für Hyperbeln und Parabeln. Siehe [[Hyperbel (Mathematik)#Hyperbel als affines Bild der Hyperbel y=1/x|Hyperbel]] und [[Parabel (Mathematik)#Eigenschaften|Parabel]]. | |||
* Falls der Kegelschnitt ''vollständig'' in einer affinen Ebene enthalten ist, gibt es auch (die am Anfang beschriebene) '''affine Form''' des Satzes, bei der die Pascalgerade die Ferngerade ist. Die affine Form gibt es z. B. in der reellen und der rationalen affinen Ebene, aber nicht in der komplexen affinen Ebene. In der komplexen projektiven Ebene schneidet jeder n.a. Kegelschnitt jede Gerade. Es gibt also keine Passante des Kegelschnitts, die man als Ferngerade wählen könnte. | |||
* Die Figur der sechs Punkte auf dem Kegelschnitt wird auch '''Hexagrammum Mysticum''' genannt.<ref>''Jacob Steiner’s Vorlesungen über synthetische Geometrie'', B. G. Teubner, Leipzig 1867 (bei Google Books: [http://books.google.de/books?id=jCgPAAAAQAAJ]), 2. Teil, S. 128. </ref> | |||
* Der Satz von Pascal ist auch für ein Geradenpaar (ausgearteter Kegelschnitt) gültig und ist dann identisch mit dem [[Satz von Pappos-Pascal]]. | |||
* Der Satz von Pascal wurde durch [[August Ferdinand Möbius]] im Jahre [[1847]] verallgemeinert: | |||
: Angenommen, ein [[Polygon]] mit <math>4n + 2</math> Seiten sei in einen Kegelschnitt einbeschrieben. Nun verlängert man die gegenüberliegenden Seiten, bis sie sich in <math>2n + 1</math> Punkten schneiden. Liegen dann <math>2n</math> dieser Punkte auf einer gemeinsamen Linie, so liegt auch der letzte Punkt auf dieser Linie. | |||
* Eine weitere Verallgemeinerung ist der [[Satz von Cayley-Bacharach]]. | |||
== Beweis des Satzes von Pascal == | |||
[[Datei:Proof-6p-pascal.svg|350px|mini|Zum Beweis des Satzes von Pascal]] | |||
Im reellen Fall kann man den Beweis am Einheitskreis führen. Da ein nichtausgearteter Kegelschnitt über einem beliebigen Körper aber nicht immer als Einheitskreis darstellbar ist, wird hier die immer mögliche Darstellung des Kegelschnitts als Hyperbel benutzt<ref>E. Hartmann: ''[http://www.mathematik.tu-darmstadt.de/~ehartmann/circlegeom.pdf Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes.]'' Skript, TH Darmstadt (PDF; 891 kB), S. 29</ref>. | |||
</ | |||
Für den Beweis koordinatisiert man die projektive Ebene [[Projektiver Kegelschnitt|inhomogen]] so, dass <math>P_1=(\infty), P_6=(0)</math> ist, d. h. die Ferngerade ist <math>g_\infty=\overline{P_1P_6} </math> (s. Bild). Ferner sei <math>P_5=(x_5,0)</math> ein Punkt der x-Achse, <math>P_2=(0,y_2)</math> ein Punkt der y-Achse. Dann gilt <math>P_9=(x_9,0)</math> und <math>P_7=(0,y_7)</math> (s. Bild). Die Steigung der Gerade <math>\overline{P_iP_k} </math> sei <math>m_{ik}</math>. Der Satz ist bewiesen, wenn <math>m_{79}=m_{43}</math> bewiesen worden ist. | |||
{{ | Man rechnet leicht nach, dass <math>\frac{m_{29}}{m_{25}}=\frac{m_{79}}{m_{75}}</math> ist. Mit <math>m_{29}=m_{23},\;m_{75}=m_{45}</math> (siehe Bild) erhält man | ||
: '''(1)'''<math>:\ m_{79}=\frac{m_{23}}{m_{25}}\cdot m_{45}</math>. | |||
Die | Der Kegelschnitt <math>\mathfrak o</math> wird in dem inhomogenen Koordinatensystem als Hyperbel mit einer Gleichung | ||
:: <math> y=\frac{a}{x-b}+c</math> beschrieben (Die Asymptoten sind parallel zu den Koordinatenachsen !). | |||
: Für solch eine Hyperbel gilt der [[Hyperbel (Mathematik)#Peripheriewinkelsatz für Hyperbeln|Peripheriewinkelsatz für Hyperbeln]]. Wendet man den Peripheriewinkelsatz auf die Grundpunkte <math>P_3,P_5</math> und die Hyperbelpunkte <math>P_2,P_4</math> an, so erhält man die Gleichung | |||
: '''(2)'''<math>:\ \frac{m_{23}}{m_{25}}=\frac{m_{43}}{m_{45}}</math>. | |||
Aus '''(1)''' und '''(2)''' ergibt sich schließlich <math>m_{79}=m_{43}</math>, was zu beweisen war. | |||
== Bedeutung des Satzes von Pascal und seiner Ausartungen == | |||
Da der Satz von Pascal eine Aussage über Kegelschnitte ist und Kegelschnitte nur in pappusschen Ebenen erklärt sind, führt man den Begriff des ''Ovals'' in einer beliebigen projektiven Ebene ein, um die Pascal-Eigenschaft in einer beliebigen projektiven Ebene formulieren zu können. Dies ist z. B. bei dem [[Satz von Pappus]] nicht nötig, da dieser ein Satz über Geraden und Punkte ist, die es in jeder projektiven Ebene gibt. Ein Oval ist eine Punktmenge (Kurve) einer projektiven Ebene mit den wesentlichen Inzidenzeigenschaften eines nicht ausgearteten Kegelschnitts. | |||
=== Definition eines Ovals === | |||
{{Hauptartikel|Oval (Projektive Geometrie)}} | |||
* Eine Menge <math>\mathfrak o</math> von Punkten in einer projektiven Ebene heißt ''Oval'', wenn | |||
: (1) Eine beliebige Gerade <math>g</math> trifft <math>\mathfrak o</math> in höchstens 2 Punkten.<br /> Falls <math>|g\cap\mathfrak o|=0</math> ist, heißt <math>g</math> ''Passante'', falls <math>|g\cap\mathfrak o|=1</math> ist, heißt <math>g</math> ''Tangente'' und falls <math>|g\cap\mathfrak o|=2</math> ist, heißt <math>g</math> ''Sekante''. | |||
: (2) Zu jedem Punkt <math>P \in \mathfrak o</math> gibt es genau eine Tangente <math>t</math>, d. h. <math> t\cap\mathfrak o=\{P\}</math>. | |||
=== Pascal-Eigenschaft eines Ovals === | |||
Ein Oval in einer beliebigen projektiven Ebene, das die im Satz von Pascal für Kegelschnitte angegebene Eigenschaft für beliebige 6 Punkte besitzt, nennt mann ''6-Punkte-pascalsch'' oder kurz ''pascalsch''. Entsprechend definiert man ''5-Punkte-pascalsch'', ''4-Punkte-pascalsch'' und ''3-Punkte-pascalsch'', falls die Aussage der 5-, 4- oder 3-Punkte-Ausartung des Satzes von Pascal für das Oval erfüllt ist (s. Bild). | |||
Die | === Bedeutungen === | ||
Die Gültigkeit der Pascal-Eigenschaft oder der 5-Punkte-Ausartung für ein Oval in einer projektiven Ebene hat dieselbe Bedeutung wie die [[Satz von Pappus|Pappus-Eigenschaft]] (für ein Geradenpaar): | |||
; Satz von [[Francis Buekenhout|Buekenhout]]<ref>F. Buekenhout: ''Plans Projectifs à Ovoides Pascaliens'', Arch. d. Math. Vol. XVII, 1966, S. 89–93.</ref>: | |||
</ | Ist <math>\mathcal P</math> eine projektive Ebene und <math>\mathfrak o</math> ein <math>\color{red}6</math>-Punkte-pascalsches Oval darin, so ist <math>\mathcal P</math> eine pappussche Ebene und <math>\mathfrak o</math> ein Kegelschnitt. | ||
; Satz von Hofmann<ref> C.E. Hofmann: ''Specelizations of Pascal's Theorem on an Oval'', Journ. o. Geom., Vol. 1/2 (1971), S. 143–153. </ref>, | |||
Ist <math>\mathcal P</math> eine projektive Ebene und <math>\mathfrak o</math> ein <math>\color{red}5</math>-Punkte-pascalsches Oval darin, so ist <math>\mathcal P</math> eine pappussche Ebene und <math>\mathfrak o</math> ein Kegelschnitt. | |||
Mit Hilfe der 4-Punkte-Ausartung und der 3-Punkte-Ausartung des Satzes von Pascal lassen sich in ''pappusschen'' Ebenen Kegelschnitte charakterisieren: | |||
; Satz<ref>E. Hartmann: ''[http://www.mathematik.tu-darmstadt.de/~ehartmann/circlegeom.pdf Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes.]'' Skript, TH Darmstadt (PDF; 891 kB), S. 32,33</ref>. | |||
: (a): Ist <math>\mathcal P</math> eine ''pappussche'' projektive Ebene und <math>\mathfrak o</math> ein '''<math>\color{magenta}4</math>'''-Punkte-pascalsches Oval darin, so ist <math>\mathfrak o</math> ein Kegelschnitt. | |||
: (b): Ist <math>\mathcal P</math> eine ''pappussche'' projektive Ebene der Charakteristik <math>\ne 2</math> und <math>\mathfrak o</math> ein '''<math>\color{blue}3</math>'''-Punkte-pascalsches Oval darin, so ist <math>\mathfrak o</math> ein Kegelschnitt. | |||
''Bemerkung:'' Wie weit man in den beiden letzten Fällen die Voraussetzung ''pappussch'' abschwächen kann, ist noch ungeklärt. Die Voraussetzung in Aussage (a) lässt sich mindestens auf ''[[Moufang-Ebene|moufangsch]]'' abschwächen. | |||
{{ | == Siehe auch == | ||
* {{WikipediaDE|Satz von Pascal}} | |||
== Literatur == | |||
* Coxeter, H. S. M., und S. L. Greitzer: ''Zeitlose Geometrie'', Klett Stuttgart, 1983 | |||
* Gerd Fischer: ''Analytische Geometrie''. 4-te Auflage, Vieweg 1985, ISBN 3-528-37235-4, S. 199 | |||
* Hanfried Lenz: ''Vorlesungen über projektive Geometrie'', Akad. Verl. Leipzig, 1965, S. 60 | |||
* Roland Stärk: ''Darstellende Geometrie'', Schöningh-Verlag, Paderborn, 1978, ISBN 3-506-37443-5, S. 114 | |||
== Weblinks == | == Weblinks == | ||
* [http://www.mathematik.tu-darmstadt.de/~ehartmann/circlegeom.pdf ''Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes''] (PDF; 891 kB), Uni Darmstadt, S. 29–35. | |||
* [http://www.mathematik.tu-darmstadt.de/~ehartmann/progeo.pdf ''Projektive Geometrie'', Kurzskript, Uni Darmstadt] (PDF; 180 kB), S. 13–16 | |||
* [http://mathgardenblog.blogspot.de/2013/06/hexagrammum-mysticum1.html hexagrammum-mysticum] | |||
* [http://www.cut-the-knot.org/Curriculum/Geometry/Pascal.shtml#words Pascal's theorem auf cut-the-knot] (englisch) | |||
== Einzelnachweise == | |||
<references /> | |||
[[Kategorie:Ebene Geometrie]] | |||
[[Kategorie:Affine Geometrie]] | |||
[[Kategorie:Projektive Geometrie]] | |||
[[Kategorie:Synthetische Geometrie]] | |||
[[Kategorie:Satz (Mathematik)|NxPascal, Satz von]] | |||
[[Kategorie:Pascal]] | |||
{{Wikipedia}} | |||
Version vom 23. August 2019, 10:19 Uhr
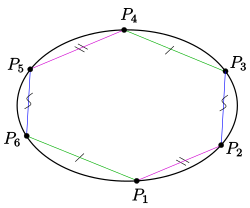



Der Satz von Pascal (nach Blaise Pascal) ist eine Aussage über ein 6-Eck auf einem nicht ausgearteten Kegelschnitt in einer projektiven Ebene. Er lässt sich in der reellen affinen Ebene wie folgt formulieren:
- Für ein 6-Eck auf einer Ellipse bei dem zwei Paare gegenüberliegender Seiten parallel sind (im Bild ), ist auch das dritte Paar gegenüberliegender Seiten parallel (im Bild: ).
Betrachtet man diesen Satz in dem projektiven Abschluss einer affinen Ebene (man nimmt die "Ferngerade", auf der sich parallele Geraden schneiden, hinzu), so gilt:
Für beliebige 6 Punkte eines nicht ausgearteten Kegelschnitts in einer projektiven Ebene liegen die Punkte
auf einer Gerade, der Pascal-Gerade (s. Bild).
Die Nummerierung gibt an, welche 6 der 15 Verbindungsgeraden der 6 Punkte benutzt werden und welche Kanten benachbart sind. Die Nummerierung ist so gewählt, dass der Kantengraph durch ein reguläres 6-Eck dargestellt werden kann. Geraden zu gegenüberliegenden Kanten des Kantengraphs werden also geschnitten. Sollen andere Kanten in die Pascalfigur eingehen, muss man die Indizes entsprechend permutieren. Für die 2. Pascal-Konfiguration wurden die Indizes 2 und 5 vertauscht (s. Bild, unten).
Nichtausgeartet heißt hier: keine 3 Punkte liegen auf einer Gerade. Den Kegelschnitt kann man sich also als Ellipse vorstellen. (Ein sich schneidendes Geradenpaar ist ein ausgearteter Kegelschnitt.)
Kegelschnitte sind nur in solchen projektiven Ebenen definiert, die sich über (kommutativen) Körpern koordinatisieren lassen. Beispiele von Körpern sind: die reellen Zahlen , die rationalen Zahlen , die komplexen Zahlen , endliche Körper. Jeder nicht ausgeartete Kegelschnitt einer projektiven Ebene lässt sich in geeigneten homogenen Koordinaten durch die Gleichung beschreiben (s. projektiver Kegelschnitt).
Bezug zu anderen Sätzen und Verallgemeinerungen

- Der Satz von Pascal ist die duale Version des Satzes von Brianchon.
- Zum Satz von Pascal gibt es Ausartungen mit 5 bzw. 4 bzw. 3 Punkten (auf einem Kegelschnitt). Bei einer Ausartung fallen zwei durch eine Kante verbundene Punkte formal zusammen und die zugehörige Sekante der Pascalfigur wird durch die Tangente in dem verbleibenden Punkt ersetzt. Siehe hierzu die Figur und weblink planar circlegeometries, S. 30–35. Durch eine geeignete Wahl einer Gerade der Pascalfiguren als Ferngerade ergeben sich Schließungssätze für Hyperbeln und Parabeln. Siehe Hyperbel und Parabel.
- Falls der Kegelschnitt vollständig in einer affinen Ebene enthalten ist, gibt es auch (die am Anfang beschriebene) affine Form des Satzes, bei der die Pascalgerade die Ferngerade ist. Die affine Form gibt es z. B. in der reellen und der rationalen affinen Ebene, aber nicht in der komplexen affinen Ebene. In der komplexen projektiven Ebene schneidet jeder n.a. Kegelschnitt jede Gerade. Es gibt also keine Passante des Kegelschnitts, die man als Ferngerade wählen könnte.
- Die Figur der sechs Punkte auf dem Kegelschnitt wird auch Hexagrammum Mysticum genannt.[1]
- Der Satz von Pascal ist auch für ein Geradenpaar (ausgearteter Kegelschnitt) gültig und ist dann identisch mit dem Satz von Pappos-Pascal.
- Der Satz von Pascal wurde durch August Ferdinand Möbius im Jahre 1847 verallgemeinert:
- Angenommen, ein Polygon mit Seiten sei in einen Kegelschnitt einbeschrieben. Nun verlängert man die gegenüberliegenden Seiten, bis sie sich in Punkten schneiden. Liegen dann dieser Punkte auf einer gemeinsamen Linie, so liegt auch der letzte Punkt auf dieser Linie.
- Eine weitere Verallgemeinerung ist der Satz von Cayley-Bacharach.
Beweis des Satzes von Pascal

Im reellen Fall kann man den Beweis am Einheitskreis führen. Da ein nichtausgearteter Kegelschnitt über einem beliebigen Körper aber nicht immer als Einheitskreis darstellbar ist, wird hier die immer mögliche Darstellung des Kegelschnitts als Hyperbel benutzt[2].
Für den Beweis koordinatisiert man die projektive Ebene inhomogen so, dass ist, d. h. die Ferngerade ist (s. Bild). Ferner sei ein Punkt der x-Achse, ein Punkt der y-Achse. Dann gilt und (s. Bild). Die Steigung der Gerade sei . Der Satz ist bewiesen, wenn bewiesen worden ist.
Man rechnet leicht nach, dass ist. Mit (siehe Bild) erhält man
- (1).
Der Kegelschnitt wird in dem inhomogenen Koordinatensystem als Hyperbel mit einer Gleichung
- beschrieben (Die Asymptoten sind parallel zu den Koordinatenachsen !).
- Für solch eine Hyperbel gilt der Peripheriewinkelsatz für Hyperbeln. Wendet man den Peripheriewinkelsatz auf die Grundpunkte und die Hyperbelpunkte an, so erhält man die Gleichung
- (2).
Aus (1) und (2) ergibt sich schließlich , was zu beweisen war.
Bedeutung des Satzes von Pascal und seiner Ausartungen
Da der Satz von Pascal eine Aussage über Kegelschnitte ist und Kegelschnitte nur in pappusschen Ebenen erklärt sind, führt man den Begriff des Ovals in einer beliebigen projektiven Ebene ein, um die Pascal-Eigenschaft in einer beliebigen projektiven Ebene formulieren zu können. Dies ist z. B. bei dem Satz von Pappus nicht nötig, da dieser ein Satz über Geraden und Punkte ist, die es in jeder projektiven Ebene gibt. Ein Oval ist eine Punktmenge (Kurve) einer projektiven Ebene mit den wesentlichen Inzidenzeigenschaften eines nicht ausgearteten Kegelschnitts.
Definition eines Ovals
- Eine Menge von Punkten in einer projektiven Ebene heißt Oval, wenn
- (1) Eine beliebige Gerade trifft in höchstens 2 Punkten.
Falls ist, heißt Passante, falls ist, heißt Tangente und falls ist, heißt Sekante. - (2) Zu jedem Punkt gibt es genau eine Tangente , d. h. .
Pascal-Eigenschaft eines Ovals
Ein Oval in einer beliebigen projektiven Ebene, das die im Satz von Pascal für Kegelschnitte angegebene Eigenschaft für beliebige 6 Punkte besitzt, nennt mann 6-Punkte-pascalsch oder kurz pascalsch. Entsprechend definiert man 5-Punkte-pascalsch, 4-Punkte-pascalsch und 3-Punkte-pascalsch, falls die Aussage der 5-, 4- oder 3-Punkte-Ausartung des Satzes von Pascal für das Oval erfüllt ist (s. Bild).
Bedeutungen
Die Gültigkeit der Pascal-Eigenschaft oder der 5-Punkte-Ausartung für ein Oval in einer projektiven Ebene hat dieselbe Bedeutung wie die Pappus-Eigenschaft (für ein Geradenpaar):
- Satz von Buekenhout[3]
Ist eine projektive Ebene und ein -Punkte-pascalsches Oval darin, so ist eine pappussche Ebene und ein Kegelschnitt.
- Satz von Hofmann[4],
Ist eine projektive Ebene und ein -Punkte-pascalsches Oval darin, so ist eine pappussche Ebene und ein Kegelschnitt.
Mit Hilfe der 4-Punkte-Ausartung und der 3-Punkte-Ausartung des Satzes von Pascal lassen sich in pappusschen Ebenen Kegelschnitte charakterisieren:
- Satz[5].
- (a): Ist eine pappussche projektive Ebene und ein -Punkte-pascalsches Oval darin, so ist ein Kegelschnitt.
- (b): Ist eine pappussche projektive Ebene der Charakteristik und ein -Punkte-pascalsches Oval darin, so ist ein Kegelschnitt.
Bemerkung: Wie weit man in den beiden letzten Fällen die Voraussetzung pappussch abschwächen kann, ist noch ungeklärt. Die Voraussetzung in Aussage (a) lässt sich mindestens auf moufangsch abschwächen.
Siehe auch
- Satz von Pascal - Artikel in der deutschen Wikipedia
Literatur
- Coxeter, H. S. M., und S. L. Greitzer: Zeitlose Geometrie, Klett Stuttgart, 1983
- Gerd Fischer: Analytische Geometrie. 4-te Auflage, Vieweg 1985, ISBN 3-528-37235-4, S. 199
- Hanfried Lenz: Vorlesungen über projektive Geometrie, Akad. Verl. Leipzig, 1965, S. 60
- Roland Stärk: Darstellende Geometrie, Schöningh-Verlag, Paderborn, 1978, ISBN 3-506-37443-5, S. 114
Weblinks
- Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF; 891 kB), Uni Darmstadt, S. 29–35.
- Projektive Geometrie, Kurzskript, Uni Darmstadt (PDF; 180 kB), S. 13–16
- hexagrammum-mysticum
- Pascal's theorem auf cut-the-knot (englisch)
Einzelnachweise
- ↑ Jacob Steiner’s Vorlesungen über synthetische Geometrie, B. G. Teubner, Leipzig 1867 (bei Google Books: [1]), 2. Teil, S. 128.
- ↑ E. Hartmann: Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes. Skript, TH Darmstadt (PDF; 891 kB), S. 29
- ↑ F. Buekenhout: Plans Projectifs à Ovoides Pascaliens, Arch. d. Math. Vol. XVII, 1966, S. 89–93.
- ↑ C.E. Hofmann: Specelizations of Pascal's Theorem on an Oval, Journ. o. Geom., Vol. 1/2 (1971), S. 143–153.
- ↑ E. Hartmann: Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes. Skript, TH Darmstadt (PDF; 891 kB), S. 32,33
| Dieser Artikel basiert (teilweise) auf dem Artikel Satz von Pascal aus der freien Enzyklopädie Wikipedia und steht unter der Lizenz Creative Commons Attribution/Share Alike. In Wikipedia ist eine Liste der Autoren verfügbar. |
















































