Eine freie Initiative von Menschen bei mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| Use Google Translate for a raw translation of our pages into more than 100 languages. Please note that some mistranslations can occur due to machine translation. |
Feld (Physik)
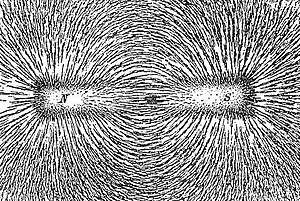
Ein Feld ist nach der physikalischen Feldtheorie ein mathematisches Modell zur Beschreibung der räumlichen Verteilung einer physikalischen Größe, welche die Feldgröße bzw. Feldstärke am jeweiligen Ort angibt. Wird dabei jedem Punkt des Raumes eine reelle Zahl (ein Skalar), zugeordnet, so spricht man von einem Skalarfeld . So kann etwa die räumliche Temperaturverteilung durch ein skalares Wärmefeld beschrieben und heute auch durch Wärmebildkameras sichtbar gemacht werden. Wird zusätzlich zum Zahlenwert auch eine Richtung angegeben, so handelt es sich um ein Vektorfeld . Das ist bei Kraftfeldern der Fall, bei denen auch die Richtung der wirkenden Kraft berücksichtigt werden muss. In den Feldtheorien werden auch häufig Tensorfelder verwendet, die als mathematische Abbildungen, jedem Punkt eines gegebenen topologischen Raumes einen Tensor zuordnen.
Ein Feld kann durch gezeichnete oder experimentell sichtbar gemachte Feldlinien dargestellt und mit den Hilfsmitteln der Differentialgeometrie berechnet werden. Ein klassisches Beispiel ist das Magnetfeld eines Magneten, das mit Eisenfeilspänen leicht sichtbar gemacht und mittels der Maxwell-Gleichungen berechnet werden kann.
Die räumlichen und zeitlichen Veränderungen eines Feldes, d.h. seine Dynamik, wird durch entsprechende Feldgleichungen beschrieben. So wird etwa das Gravitationsfeld in der allgemeinen Realativitätstheorie durch die Einsteinschen Feldgleichungen dargestellt.
Feldtypen
Die Feldtheorie unterscheidet zwischen zwei Typen von Feldern, die als Quellenfelder und Wirbelfelder bezeichnet werden. Im allgemeinen Fall ist auch eine Kombination dieser beiden Typen möglich.
Quellenfeld
Quellenfeldern, wie etwa das Gravitationsfeld oder das elektrostatische Feld, verfügen über Quellen und Senken, die die Ausgangs- bzw. Endpunkte der Feldlinien bzw. Strömungen darstellen.
Die Rotation eines wirbelfreien Vektorfeldes ist gleich Null:
Das Feld ist dann, als Kraftfeld aufgefasst, konservativ, d. h. es wird auf einem geschlossenen Weg keine Arbeit verrichtet. Damit ist auch das zugehörige Kurvenintegral gleich Null:
Ein wirbelfreies Vektorfeld lässt sich stets auch als Gradient eines zugrundeliegenden skalaren Felds formulieren, d. h. als Gradientenfeld bzw. Potentialfeld eines Skalarpotentials:
Wirbelfeld
Wirbelfelder, wie etwa das Magnetfeld, besitzen keine Quellen und Senken, da ihre Feldlinien in sich geschlossene Kurven bilden. Daher ist die Divergenz der magnetischen Flussdichte gleich Null:
Siehe auch
- Feld (Physik) - Artikel in der deutschen Wikipedia
- Feldtheorie - Artikel in der deutschen Wikipedia






















