Goldener Schnitt

Proportionen beim Goldenen Schnitt einer Strecke:$\Phi ={\frac {a}{b}}={\frac {a+b}{a}}$

Als Goldener Schnitt (lateinisch: sectio aurea, proportio divina) wird das Teilungsverhältnis einer Strecke oder anderen Größe bezeichnet, bei dem das Verhältnis des Ganzen zu seinem größeren Teil (auch Major genannt) dem Verhältnis des größeren zum kleineren Teil (dem Minor) entspricht. Als Formel ausgedrückt (mit $a$ als Major und $b$ als Minor) gilt:

${\frac {a+b}{a}}={\frac {a}{b}}$ oder ${\frac {a}{a+b}}={\frac {b}{a}}$

Das mittels Division dieser Größen als Zahl berechnete Teilungsverhältnis des Goldenen Schnittes ist eine irrationale Zahl, das heißt eine Zahl, die sich nicht als Bruch ganzer Zahlen darstellen lässt. Diese Zahl wird ebenfalls als Goldener Schnitt oder auch als Goldene Zahl bezeichnet. Als mathematisches Symbol für diese Zahl wird meist der griechische Buchstabe Phi ($\Phi$, $\phi$ oder $\varphi$), seltener auch Tau ($\mathrm {T}$, $\tau$) oder $g$ verwendet:

$\Phi ={\frac {a}{b}}={\frac {a+b}{a}}$

Die Kenntnis des Goldenen Schnittes ist in der mathematischen Literatur seit der Zeit der griechischen Antike (Euklid von Alexandria) nachgewiesen. Vereinzelt schon im Spätmittelalter (Campanus von Novara) und besonders dann in der Renaissance (Luca Pacioli, Johannes Kepler) wurde er auch in philosophische und theologische Zusammenhänge gestellt. Seit dem 19. Jahrhundert wurde er zunächst in der ästhetischen Theorie (Adolf Zeising) und dann auch in künstlerischer, architektonischer und kunsthandwerklicher Praxis als ein ideales Prinzip ästhetischer Proportionierung bewertet. Die Nachweisbarkeit einer derart besonderen ästhetischen Wirkung ist in der Forschung allerdings umstritten, desgleichen die historische Frage, ob der Goldene Schnitt auch schon bei der Proportionierung von Kunst- und Bauwerken älterer Epochen eine Rolle gespielt hat.

Das Verhältnis des goldenen Schnitts ist nicht nur in Mathematik, Kunst oder Architektur von Bedeutung, sondern findet sich auch in der Natur, beispielsweise bei der Anordnung von Blättern und in Blütenständen mancher Pflanzen wieder.

Definition und elementare Eigenschaften

Beide Rechtecke sind Goldene Rechtecke (animierte Darstellung)

Eine Strecke ${\overline {AB}}$ der Länge $s$ wird durch einen inneren Punkt $T$ so geteilt, dass das Verhältnis der Länge $a$ des größeren Teilabschnitts ${\overline {AT}}$ zur der Länge $b$ des kleineren Teilabschnitts ${\overline {TB}}$ dem Verhältnis der gesamten Streckenlänge $s=a+b$ zur Länge $a$ des größeren Teilabschnitts entspricht. Es gilt somit ${\overline {AB}}:{\overline {AT}}={\overline {AT}}:{\overline {TB}}$ beziehungsweise $(a+b):a=a:b$. Diese Teilung heißt Goldener Schnitt der Strecke ${\overline {AB}}$. Man spricht dann davon, dass der Punkt $T$ die Strecke ${\overline {AB}}$ im Goldenen Schnitt teilt oder auch von der stetigen Teilung der Stecke ${\overline {AB}}$ durch den Punkt $T$. Das Verhältnis $a:b$ der Streckenabschnitte ${\overline {AB}}$ und ${\overline {TB}}$ wird Goldene Zahl genannt.

Eine einfache Rechnung zeigt:

$\Phi ={\frac {a}{b}}={\frac {1+{\sqrt {5}}}{2}}\approx 1{,}6180339887$

Wird eine Strecke $s$ im Goldenen Schnitt geteilt, so gilt für den längeren Abschnitt

$a={\frac {s}{\Phi }}={\frac {-1+{\sqrt {5}}}{2}}s=(\Phi -1)s\approx 0{,}618s$

und für den kürzeren

$b=s-{\frac {s}{\Phi }}={\frac {3-{\sqrt {5}}}{2}}s\approx 0{,}382s$

$b={\frac {s}{\Phi ^{2}}}={\frac {4}{6+2{\sqrt {5}}}}s\approx 0{,}382s.$

Die Goldene Zahl ist eine irrationale Zahl, das heißt, sie lässt sich nicht als Bruch zweier ganzer Zahlen darstellen. Sie ist jedoch eine algebraische Zahl vom Grad 2, insbesondere kann sie mit Zirkel und Lineal konstruiert werden.

Geometrische Aussagen

Konstruktionen mit Zirkel und Lineal

Als Konstruktionsverfahren werden nach den Postulaten des Euklid nur diejenigen Verfahren akzeptiert, die sich auf die Verwendung von Zirkel und Lineal (ohne Skala) beschränken. Für die Teilung einer Strecke im Verhältnis des Goldenen Schnittes gibt es eine Fülle derartiger Verfahren, von denen im Folgenden exemplarisch nur einige erwähnt werden. Unterschieden wird dabei eine innere und äußere Teilung. Bei der äußeren Teilung wird der in der Verlängerung der Ausgangsstrecke außen liegende Punkt gesucht, der die vorhandene Strecke zum (größeren) Teil des Goldenen Schnittes macht. Der Goldene Schnitt stellt dabei einen Spezialfall der harmonischen Teilung dar. Aufgeführt werden im Folgenden auch zwei moderne, von Künstlern gefundene Konstruktionen.

Innere Teilung

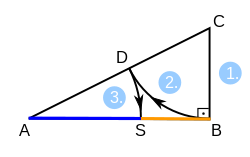Klassische innere Teilung	Klassisches Verfahren mit innerer Teilung, das wegen seiner Einfachheit beliebt ist: Errichte auf der Strecke AB im Punkt B eine Senkrechte der halben Länge von AB mit dem Endpunkt C. Der Kreis um C mit dem Radius CB schneidet die Verbindung AC im Punkt D. Der Kreis um A mit dem Radius AD teilt die Strecke AB im Verhältnis des Goldenen Schnittes.
	Innere Teilung nach Euklid: Goldener Schnitt, innere Teilung nach Euklid Johann Friedrich Lorenz beschrieb im Jahr 1781 in seinem Buch Euklids Elemente folgende Aufgabenstellung von Euklid: „Eine gegebne gerade Linie, AB, so zu schneiden, daß das Rectangel aus der Ganzen und Einem der Abschnitte, dem Quadrat des anderen Abschnitts gleich sey.“ Das Ergebnis der nebenstehenden Animation zeigt, die Strecke ${\overline {AB}}$ ist in einem Verhältnis geteilt, das man heute als den Goldenen Schnitt mit innerer Teilung bezeichnet. Als Darstellung dieses Verfahrens hat sich eine vereinfachte Konstruktion, siehe linkes Bild, bewährt: Errichte auf der Strecke AB im Punkt A eine Senkrechte der halben Länge von AB mit dem Endpunkt C. Der Kreis um C mit dem Radius CB schneidet die Verlängerung von AC im Punkt D. Der Kreis um A mit dem Radius AD teilt die Strecke AB im Verhältnis des Goldenen Schnittes.
	Konstruktion nach dem österreichischen Künstler Kurt Hofstetter, die dieser 2005 im Forum Geometricorum publizierte: Halbiere die Strecke AB in M durch Streckensymmetrale mit Radius AB und konstruiere dabei ein gleichseitiges Dreieck ABC mit der Seitenlänge AB und C unterhalb von AB. Konstruiere ein gleichschenkeliges Dreieck MBD mit Schenkellänge AB über der Grundlinie MB Die Strecke CD teilt die Strecke AB im Verhältnis des Goldenen Schnittes.

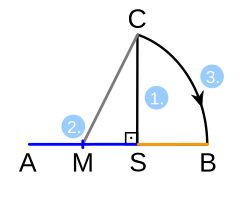
Äußere Teilung

Klassisches Verfahren mit äußerer Teilung: Errichte auf der Strecke AS im Punkt S eine Senkrechte der Länge AS mit dem Endpunkt C. Konstruiere die Mitte M der Strecke AS. Der Kreis um M mit dem Radius MC schneidet die Verlängerung von AS im Punkt B. S teilt AB im Verhältnis des Goldenen Schnittes. Nebenstehendes Beispiel: Fünfeck bei gegebener Seitenlänge B ${\widehat {=}}$ A, G ${\widehat {=}}$ M, A ${\widehat {=}}$ S, H ${\widehat {=}}$ C und J ${\widehat {=}}$ B. (Beispiel: B des rechten Bildes ${\widehat {=}}$ A des linken Bildes)

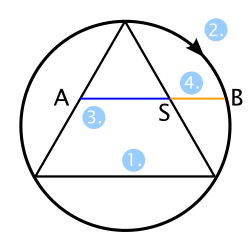
Konstruktion nach dem amerikanischen Künstler George Odom, die dieser 1982 entdeckte: Konstruiere ein gleichseitiges Dreieck. Konstruiere den Umkreis, also den Kreis, der durch alle Ecken des Dreiecks verläuft. Halbiere zwei Seiten des Dreiecks in den Punkten A und S. Die Verlängerung von AS schneidet den Kreis im Punkt B. S teilt AB im Verhältnis des Goldenen Schnittes. Begonnen wird mit der Strecke AS, so wird über der halben Strecke das in S rechtwinklige Dreieck mit dem Umkreismittelpunkt (Höhe: AS/2, 2. Kathete: AS) konstruiert.

Anstatt stets neu konstruieren zu müssen, wurde im 19. Jahrhundert von Künstlern und Handwerkern ein Goldener Zirkel – ein auf das Goldene Verhältnis eingestellter Reduktionszirkel – benutzt. Insbesondere im Schreinerhandwerk wurde ein ähnliches Instrument in Form eines Storchschnabels benutzt.

Der Goldene Schnitt im Fünfeck und im Pentagramm

Pentagramm

→ Hauptartikel: Pentagramm und Fünfeck

Regelmäßiges Fünfeck und Pentagramm bilden jeweils eine Grundfigur, in der das Verhältnis des Goldenen Schnittes wiederholt auftritt. Die Seite eines regelmäßigen Fünfecks z. B. befindet sich im Goldenen Schnitt zu seinen Diagonalen. Die Diagonalen untereinander wiederum teilen sich ebenfalls im goldenen Verhältnis, d. h. ${\overline {AD}}$ verhält sich zu ${\overline {BD}}$ wie ${\overline {BD}}$ zu ${\overline {CD}}$. Der Beweis dazu nutzt die Ähnlichkeit geeignet gewählter Dreiecke.

Das Pentagramm, eines der ältesten magischen Symbole der Kulturgeschichte, steht in einer besonders engen Beziehung zum Goldenen Schnitt. Zu jeder Strecke und Teilstrecke im Pentagramm findet sich ein Partner, der mit ihr im Verhältnis des Goldenen Schnittes steht. In der Abbildung sind alle drei möglichen Streckenpaare jeweils blau (längere Strecke) und orange (kürzere Strecke) markiert. Sie lassen sich über das oben beschriebene Verfahren der stetigen Teilung nacheinander erzeugen. Im Prinzip ist es damit in das verkleinerte Pentagramm fortsetzbar, das in das innere Fünfeck gezeichnet werden könnte, und damit in alle weiteren. Stünden die beiden Strecken in einem Verhältnis ganzer Zahlen, müsste dieses Verfahren der fortgesetzten Subtraktion irgendwann Null ergeben und damit abbrechen. Die Betrachtung des Pentagramms zeigt aber anschaulich, dass das nicht der Fall ist. Eine Weiterentwicklung dieser Geometrie findet sich bei der Penrose-Parkettierung.

Für den Beweis, dass es sich um den Goldenen Schnitt handelt, beachte man, dass neben den vielen Strecken, die aus offensichtlichen Symmetriegründen gleich lang sind, auch ${\overline {\mathrm {CD} }}={\overline {\mathrm {CC'} }}$ gilt. Ursache ist, dass das Dreieck $DCC^{\prime }$ zwei gleiche Winkel besitzt, wie durch Parallelverschiebung der Strecke $CC^{\prime }$ erkannt werden kann, und daher gleichschenklig ist. Nach dem Strahlensatz gilt:

${\frac {\overline {\mathrm {AB} }}{\overline {\mathrm {BB'} }}}={\frac {\overline {\mathrm {AC} }}{\overline {\mathrm {CC'} }}}$

Wird ${\overline {\mathrm {AC} }}={\overline {\mathrm {AB} }}+{\overline {\mathrm {BC} }}$ ersetzt und die Gleichheit der auftretenden Teilstücke beachtet, so wird genau die obige Definitionsgleichung für den Goldenen Schnitt erhalten.

Goldenes Rechteck und Goldenes Dreieck

Ein Rechteck, dessen Seitenverhältnis dem Goldenen Schnitt entspricht, wird als Goldenes Rechteck benannt und ebenso ein gleichschenkliges Dreieck, bei dem zwei Seiten in diesem Verhältnis stehen, als Goldenes Dreieck.

• Zum Vergleich von Rechtecksproportionen siehe Abschnitt Vergleich mit anderen prominenten Seitenverhältnissen.
• Ein Goldenes Dreieck ist Inhalt der Methode innere Teilung im Abschnitt Konstruktionen mit Zirkel und Lineal,

Goldener Winkel

Der Goldene Winkel ($\approx 137{,}5^{\circ }$) ist der Kreiswinkel des kleineren Kreisbogens $b$, wenn er mit dem größeren Kreisbogen $a$ einen Kreis vom Umfang $a+b$ bildet und das Verhältnis $a:b$ dem Goldenen Schnitt entspricht.

Blattstand einer Pflanze mit einem Blattabstand nach dem Goldenen Winkel

Der Goldene Winkel wird erhalten, wenn der Vollwinkel im Goldenen Schnitt geteilt wird. Dies führt auf den überstumpfen Winkel ${\tfrac {2\pi }{\Phi }}\approx 3{,}88\approx 222{,}5^{\circ }.$ Gewöhnlich wird aber seine Ergänzung zum Vollwinkel, $2\pi -{\tfrac {2\pi }{\Phi }}\approx 2{,}40\approx 137{,}5^{\circ }$ als Goldener Winkel bezeichnet. Dies ist dadurch gerechtfertigt, dass Drehungen um $\pm 2\pi$ keine Rolle spielen und das Vorzeichen nur den Drehsinn des Winkels bezeichnet.

Durch wiederholte Drehung um den Goldenen Winkel entstehen immer wieder neue Positionen, etwa für die Blattansätze im Bild. Wie bei jeder irrationalen Zahl werden dabei nie exakte Überdeckungen entstehen. Weil die Goldene Zahl im unten beschriebenen Sinn die „irrationalste“ Zahl darstellt, wird dabei erreicht, dass die Überdeckung der Blätter, welche die Photosynthese behindert, in der Summe minimiert wird.

Dabei zerlegen die ersten $n$ Positionen den Kreis in $n$ Abschnitte. Diese $n$ Abschnitte haben höchstens drei verschiedene Winkel. Im Fall einer Fibonacci-Zahl $n=f_{k}$ treten nur zwei Winkel ${\tfrac {2\pi }{\Phi ^{k-1}}},{\tfrac {2\pi }{\Phi ^{k}}}$ auf. Für $f_{k}<n<f_{k+1}$ tritt der Winkel ${\tfrac {2\pi }{\Phi ^{k+1}}}$ hinzu.

Betrachtet man für wachsendes $n$ fortfolgend die sich verfeinernden Zerlegungen des Kreises, so teilt die $(n+1)$-te Position stets einen der verbliebenen größten Abschnitte, und zwar immer den im Verlauf der Teilungen zuerst entstandenen, d. h. den „ältesten“ Abschnitt. Diese Teilung erfolgt im goldenen Verhältnis, sodass, im Uhrzeigersinn gesehen, ein Winkel ${\tfrac {2\pi }{\Phi ^{l}}}$ mit geradem $l$ vor einem Winkel ${\tfrac {2\pi }{\Phi ^{l\pm 1}}}$ mit ungeradem $l\pm 1$ liegt.

Wenn wir den Abschnitt mit dem Winkel ${\tfrac {2\pi }{\Phi ^{k}}}$ mit $w_{k}$ bezeichnen, so erhalten wir so nacheinander die Kreiszerlegungen $w_{0},$ $w_{2}w_{1},$ $w_{2}w_{2}w_{3},$ $w_{4}w_{3}w_{2}w_{3},$ $w_{4}w_{3}w_{4}w_{3}w_{3},$ $w_{4}w_{3}w_{4}w_{3}w_{4}w_{5},$ $w_{4}w_{4}w_{5}w_{4}w_{3}w_{4}w_{5},$ $w_{4}w_{4}w_{5}w_{4}w_{4}w_{5}w_{4}w_{5},$ $w_{6}w_{5}w_{4}w_{5}w_{4}w_{4}w_{5}w_{4}w_{5},$ $w_{6}w_{5}w_{4}w_{5}w_{6}w_{5}w_{4}w_{5}w_{4}w_{5}$ usw.

Goldene Spirale

Goldene Spirale, genähert durch Viertelkreise. Das Verhältnis der Radien der Kreissektoren entspricht der Fibonacci-Folge.

Die Goldene Spirale ist ein Sonderfall der logarithmischen Spirale. Diese Spirale lässt sich mittels rekursiver Teilung eines Goldenen Rechtecks in je ein Quadrat und ein weiteres, kleineres Goldenes Rechteck konstruieren (siehe nebenstehendes Bild). Sie wird oft durch eine Folge von Viertelkreisen approximiert. Ihr Radius ändert sich bei jeder 90°-Drehung um den Faktor $\Phi$.

Es gilt

$\textstyle r(\theta )=ae^{k\theta }=a\Phi ^{\frac {2\theta }{\pi }}$

mit der Steigung $\textstyle k=\pm {\frac {\ln {\Phi }}{\alpha _{\llcorner }}}$, wobei $\alpha _{\llcorner }$ hierbei der Zahlenwert für den rechten Winkel, also 90° bzw. ${\tfrac {\pi }{2}}$ ist, also $\textstyle k={\frac {2\ln(\Phi )}{\pi }}$ mit der Goldenen Zahl $\textstyle \Phi ={\frac {{\sqrt {5}}+1}{2}}$.

Mithin gilt für die Steigung:

$\textstyle |k|\approx 0{,}005346798/{}^{\circ }\approx 0{,}30634896/\mathrm {rad}$

Die Goldene Spirale ist unter den logarithmischen Spiralen durch die folgende Eigenschaft ausgezeichnet. Seien $P_{1},P_{2},P_{3},P_{4}$ vier auf der Spirale aufeinanderfolgende Schnittpunkte mit einer Geraden durch das Zentrum. Dann sind die beiden Punktepaare $P_{1},P_{4}$ und $P_{2},P_{3}$ harmonisch konjugiert, d. h., für ihr Doppelverhältnis gilt

$(P_{\theta },P_{\theta +3\pi };P_{\theta +\pi },P_{\theta +2\pi })={\frac {(-\Phi ^{6}-\Phi ^{4})(-\Phi ^{2}-1)}{(-\Phi ^{6}+\Phi ^{2})(\Phi ^{4}-1)}}={\frac {-\Phi ^{2}}{(-\Phi ^{2}+1)^{2}}}=-1.$

Zu weitere Themen siehe auch

• Goldener Schnitt - Artikel in der deutschen Wikipedia

Siehe auch

• Goldener Schnitt - Artikel in der deutschen Wikipedia
• Silberner Schnitt - Artikel in der deutschen Wikipedia
• Harmonische Teilung - Artikel in der deutschen Wikipedia, eine weitere Teilung der Ästhetik
• Mathematische Konstanten - Artikel in der deutschen Wikipedia
• Liste besonderer Zahlen - Artikel in der deutschen Wikipedia
• Fibonacci-Folge - Artikel in der deutschen Wikipedia

Literatur

Historische Literatur

• Luca Pacioli; Constantin Winterberg (Hrsg. und Übers.): De divina proportione. Venedig 1509. Carl Graeser, Wien 1889 (im Internet-Archiv: Online, bei alo: Online.)
• Adolf Zeising: Neue Lehre von den Proportionen des menschlichen Körpers. Rudolph Weigel, Leipzig 1854 (bei Google Books.)
• Adolf Zeising: Das Normalverhältniss der chemischen und morphologischen Proportionen. Rudolph Weigel, Leipzig 1856 (bei Google Books.)
• Gustav Theodor Fechner: Zur experimentalen Ästhetik. Hirzel, Leipzig 1871.

Neuere Literatur

• Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg/Berlin/Oxford 1996. ISBN 3-86025-404-9.
• Priya Hemenway: Divine Proportion. Phi in Art, Nature and Science. Sterling, New York 2005, ISBN 1-4027-3522-7. ( Priya Hemenway: Der Geheime Code: Die rätselhafte Formel, die Kunst, Natur und Wissenschaft bestimmt. Taschen Verlag, Köln 2008, ISBN 978-3-8365-0708-0.)
• Roger Herz-Fischler: A mathematical History of the Golden Ratio. Dover Publications, New York 1998, ISBN 0-486-40007-7.
• Jürgen Fredel: Maßästhetik. Studien zu Proportionsfragen und zum Goldenen Schnitt. Lit, Hamburg 1998, ISBN 3-8258-3408-5.
• Albert van der Schoot: Die Geschichte des goldenen Schnitts. Aufstieg und Fall der göttlichen Proportion. Frommann-Holzboog, Stuttgart 2005, ISBN 3-7728-2218-5.

  Susanne Deicher: Rezension von: Albert van der Schoot: Die Geschichte des goldenen Schnitts. In: sehepunkte 5 (2005), Nr. 12 [15. Dezember 2005], Weblink.

• Hans Walser: Der Goldene Schnitt. Teubner, Stuttgart 1993. ISBN 3-8154-2511-5.
• Georg Markowsky: Misconceptions about the Golden Mean. (PDF; 2,05 MB). The College Mathematics Journal, Band 23, Ausgabe 1, Januar 1992.
• Clement Falbo: The Golden Ratio: A Contrary Viewpoint. (PDF; 625 kB). The College Mathematics Journal, Band 36, Ausgabe 2, März 2005.

Weblinks

Commons: Goldener Schnitt – Weitere Bilder oder Audiodateien zum Thema

Deutsch

• Marcus Frings: Goldener Schnitt. In: Reallexikon zur Deutschen Kunstgeschichte (RDK) Labor (2015).
• Bernhard Peter: Goldener Schnitt – Mathematik und Bedeutung. (34 verschiedene Konstruktionsverfahren, Bedeutung in der Kunst; private Seite).
• Ruben Stelzner: Der goldene Schnitt – Das Mysterium der Schönheit. (2002).
• Bilder zum Goldenen Schnitt in der Biologie (private Seite).
• Joachim Mohr: Die stetige Teilung oder der goldene Schnitt und die Konstruktion des regelmäßigen Fünfecks.
• Der Goldene Schnitt und sein Vorkommen in der heutigen Welt YouTube

Englisch

• Marcus Frings: The Golden Section in Architectural Theory. In: Nexus Network Journal. 4/1 (2002).
• Eric W. Weisstein: Golden Ratio. In: MathWorld (englisch).
• John J. O’Connor, Edmund F. Robertson: The Golden Ratio. In: MacTutor History of Mathematics archive (englisch)
• Alexander Bogomolny: Golden Ratio. Auf: cut-the-knot.org-
• Steven Strogatz: Proportion Control. New York Times (Online), 24. September 2012.

Einzelnachweise

• Albrecht Beutelspacher, Bernhard Petri: Der Goldene Schnitt. Spektrum, Heidelberg, Berlin, Oxford 1988. ISBN 3-411-03155-7.