Kegel (Geometrie)

Gerader Kreiskegel (links) und schiefer Kreiskegel

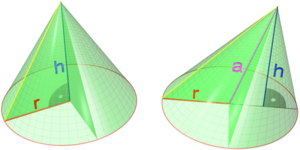
Ein Kegel oder Konus ist ein geometrischer Körper, der entsteht, wenn man alle Punkte eines in einer Ebene liegenden, begrenzten und zusammenhängenden Flächenstücks geradlinig mit einem Punkt (Spitze bzw. Apex) außerhalb der Ebene verbindet. Ist das Flächenstück eine Kreisscheibe, wird der Körper Kreiskegel genannt. Das Flächenstück nennt man Grundfläche, deren Begrenzungslinie die Leitkurve und den Punkt die Spitze oder den Scheitel des Kegels. Ein Kegel hat also eine Spitze (den Scheitelpunkt), eine Kante (die Leitkurve) und zwei Flächen (die Mantel- und die Grundfläche).

Unter der Höhe des Kegels versteht man einerseits das Lot von der Spitze auf die Grundfläche (die Höhe steht also immer senkrecht zur Grundfläche), andererseits aber auch die Länge dieses Lotes (also den Abstand der Spitze von der Grundfläche).

Die Verbindungsstrecken der Spitze mit der Leitkurve heißen Mantellinien, ihre Vereinigung bildet den Kegelmantel oder die Mantelfläche.

Gerader und schiefer Kegel

Wenn in der Geometrie von einem Kegel gesprochen wird, ist häufig der Spezialfall des geraden Kreiskegels gemeint. Unter einem Kreiskegel versteht man einen Körper, der durch einen Kreis (Grundkreis oder Basiskreis) und einen Punkt außerhalb der Ebene des Kreises (Spitze des Kegels) festgelegt ist.

Die Ebene, in welcher der Basiskreis liegt, heißt Basis(kreis)ebene. Unter dem Radius $r$ des Kegels versteht man normalerweise den Radius des Basiskreises. Die Gerade durch den Mittelpunkt des Grundkreises und die Spitze nennt man die Achse des Kegels. Die Höhe $h$ des Kegels ist der Abstand der Spitze von der Basisebene; dieser Abstand muss senkrecht zur Basisebene gemessen werden.

Steht die Achse senkrecht zur Basisebene, so liegt ein gerader Kreiskegel oder Drehkegel vor. Andernfalls spricht man von einem schiefen Kreiskegel oder elliptischen Kegel. Jeder elliptische Kegel hat zwei Richtungen, in denen sein Schnitt mit einer Ebene ein Kreis ist; diese Tatsache macht sich die stereografische Projektion als Kreistreue zunutze.

Die Bezeichnung „Drehkegel“ deutet darauf hin, dass es sich um einen Rotationskörper handelt. Er entsteht durch Rotation eines rechtwinkligen Dreiecks um eine seiner beiden Katheten. In diesem Fall werden die Mantellinien (also die Verbindungsstrecken der (Rand-) Punkte des Basiskreises mit der Spitze) auch Erzeugende genannt ($s$), da sie den Mantel „erzeugen“. Der Öffnungswinkel beträgt das Doppelte des Winkels zwischen den Mantellinien und der Achse eines Drehkegels. Der Winkel $\varphi$ zwischen den Mantellinien und der Achse heißt halber Öffnungswinkel.

Ein Drehkegel mit Öffnungswinkel 60° heißt gleichseitiger Kegel. Diese Bezeichnung erklärt sich wie folgt: Schneidet man einen solchen Kegel mit einer Ebene, die die Achse enthält, so erhält man ein gleichseitiges Dreieck.

Vor allem in der Technik wird für den Drehkegel auch das Wort Konus (von lat. conus) verwendet. Das zugehörige Eigenschaftswort konisch bezeichnet Objekte mit der Form eines Drehkegels oder eines (Dreh-) Kegelstumpfs.

Insbesondere im Zusammenhang mit Kegelschnitten wird das Wort „Kegel“ auch im Sinn des nachstehend erwähnten Doppelkegels gebraucht.

Doppelkegel

Doppelkegel mit gegeneinander gerichteten Spitzen, einer Sanduhr ähnlich

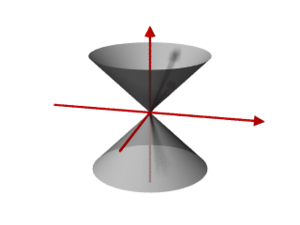
Ein Doppelkegel entsteht als Rotationsfläche einer Geraden um eine sie nicht rechtwinkelig schneidende Achse. Es entstehen zwei Drehkegel mit dem gleichen Öffnungswinkel und einer gemeinsamen Achse, die sich in der Spitze berühren. Schneidet man einen solchen unendlichen Doppelkegel mit einer Ebene, entstehen die Kegelschnitte: Kreis, Ellipse, Parabel, Hyperbel.

Zu etlichen weiteren Theman siehe auch

• Kegel (Geometrie) - Artikel in der deutschen Wikipedia

Siehe auch

• Kegel (Geometrie) - Artikel in der deutschen Wikipedia