Jeden Dienstag live ab 19h. Die Vorträge sind frei zugänglich und können wenig später auch als Video, Audio und als transkripierter Text abgerufen werden.
Neuer Link:https://sichere-videokonferenz.de/Ahuameo6JnF5h (läuft ohne Zeitlimit auf einem deutschen Server mit der gewohnten Jitsi-Software). Wenn du "neu" bist, bitte kontaktiere Wolfgang oder François im Voraus über die dir bekannten Kontaktmöglichkeiten oder übers Kontaktformular. Um Störungen zu vermeiden: Bitte schalte das Mikrofon vor Eintreten stumm. Unser Miteinander ist persönlich- bitte mit Kamera und Vornamen einloggen.
Alternativ kannst du hier live im youtube schauen:
Die fünf platonischen Körper als Kunstobjekte im Bagno Steinfurt
Die Platonischen Körper (nach dem griechischen Philosophen Platon) sind die Polyeder mit größtmöglicher Symmetrie. Jeder von ihnen wird von mehreren deckungsgleichen (kongruenten) ebenen regelmäßigen Vielecken begrenzt. Eine andere Bezeichnung ist reguläre Körper (von lat.corpora regularia[1][2]).
Es gibt fünf platonische Körper. Ihre Namen enthalten die griechisch ausgedrückte Zahl ihrer begrenzenden Flächen und eder als Abwandlung des griechischen Wortes ἕδρα (hedra) (s.auch Polyeder), deutsch (Sitz-)Fläche.
Tetraeder (Vierflächner, Oberfläche aus vier Dreiecken)
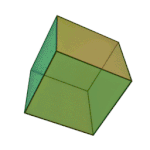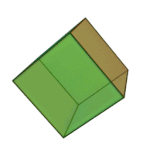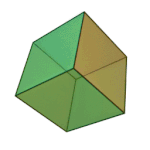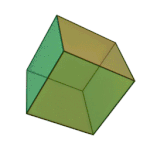
Hexaeder (Sechsflächner, Oberfläche aus sechs Quadraten) – der Würfel
Oktaeder (Achtflächner, Oberfläche aus acht Dreiecken)
Dodekaeder (Zwölfflächner, Oberfläche aus zwölf Fünfecken) – auch Pentagondodekaeder genannt, um auf die Oberfläche aus Fünfecken als seine Besonderheit hinzuweisen
Ikosaeder (Zwanzigflächner, Oberfläche aus zwanzig Dreiecken)
Die Platonischen Körper sind konvex.
In jeder Ecke des Körpers treffen jeweils gleich viele gleich lange Kanten zusammen, an jeder Kante treffen sich zwei deckungsgleiche Flächen, und jede Fläche hat gleich viele Ecken. Es ist also nicht möglich, irgendwelche zwei Körperecken, Kanten und Flächen aufgrund von Beziehungen zu anderen Punkten des Polyeders voneinander zu unterscheiden.
Verzichtet man auf die Ununterscheidbarkeit der Flächen und Kanten, spricht man von archimedischen Körpern. Verzichtet man dagegen auf die Ununterscheidbarkeit der Ecken und Kanten, spricht man von catalanischen Körpern. Verzichtet man auf die Konvexität, spricht man von regulären Polyedern und schließt damit die Kepler-Poinsot-Körper ein.
Paul Adam, Arnold Wyss: Platonische und Archimedische Körper, ihre Sternformen und polaren Gebilde. Verlag Freies Geistesleben, Stuttgart 1984, ISBN 3-7725-0965-7
Renatus Ziegler: Platonische Körper. Verwandtschaften, Metamorphosen, Umstülpungen. Verlag am Goetheanum, Dornach/Schweiz 2012, ISBN 978-3-7235-1326-2
anthrowiki.at, 
anthro.world, 
biodyn.wiki und 
steiner.wiki
Wie Sie die Entwicklung von AnthroWiki durch Ihre Spende unterstützen können, erfahren Sie hier.
Commons: Platonische Körper – Weitere Bilder oder Audiodateien zum Thema
Wikiversity: Die Symmetriegruppen der platonischen Körper – Kursmaterialien, Forschungsprojekte und wissenschaftlicher Austausch
Wiktionary: platonischer Körper – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen
