Eine freie Initiative von Menschen bei mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| Use Google Translate for a raw translation of our pages into more than 100 languages. Please note that some mistranslations can occur due to machine translation. |
Drehimpuls
Der Drehimpuls oder , in der Mechanik auch als Drall oder veraltet als Schwung oder Impulsmoment bezeichnet ist eine mit Drehbewegungen (Rotationen) verbundene vektorielle physikalische Erhaltungsgröße mit der Dimension Masse × Länge × Geschwindigkeit und wird im SI-System in Joulesekunden () gemessen. Er hat damit die gleiche Dimension wie die Wirkung. Die Drehimpulserhaltung folgt nach dem 1918 von Emmy Noether formulierten Noether-Theorem aus der Isotropie des Raumes, also aus der Rotationsinvarianz, nach der keine Richtung im Raum eine bevorzugte Rolle spielt.
Im Allgemeinen setzt sich der Drehimpuls aus zwei Komponenten zusammen, nämlich aus dem Eigendrehimpuls des bewegten Körpers und dem Bahndrehimpuls auf seiner Bahn relativ zu einem Bezugspunkt (dem Rotationszentrum).
Definition
Mathematisch ist der Drehimpulsvektor als Vektorprodukt des Ortsvektors und des Impulsvektors definiert:
Quantenmechanik
Der Gesamtdrehimpuls eines quantenmechanischen Systems kann bestimmte diskrete Werte annehmen und setzt sich aus dem Bahndrehimpulsoperator und dem Spinoperator zusammen.
Bahndrehimpuls
Der Bahndrehimpuls eines quantenmechanischen Systems wird durch die Drehimpulsquantenzahl oder Nebenquantenzahl bestimmt, die Aufschluss über die Form der Bahn bzw. des Atomorbitals gibt. Die Nebenquantenzahlen und die ihnen entsprechenden Orbitale werden üblicherweise auch mit folgenden Buchstaben bezeichnet, die historisch aus der Spektroskopie übernommen wurden:
- s für (ursprünglich für ‚scharf‘, z. B. „s-Zustand“)
- p für (ursprünglich für engl. ‚principal‘, ‚Haupt‘-Zustand)
- d für (ursprünglich für ‚diffus‘)
- f für (ursprünglich für ‚fundamental‘)
- g für
Der Bahndrehimpuls unterliegt in einem Magnetfeld einer durch die Richtungsquantenzahlen (auch magnetische Quantenzahlen genannt) bestimmten Richtungsquantelung, durch die er nur die diskreten Werte annehmen kann. Für die erlaubten Winkel bezüglich einer ausgezeichneten Bezugsachse gilt dann:
- .
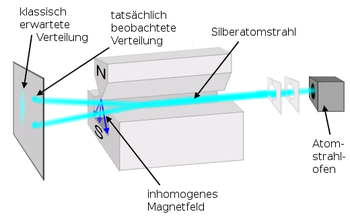
Erstmals beobachtet wurde die Richtungsquantelung bei dem 1922 durchgeführten Stern-Gerlach-Experiment durch die unterschiedliche, gequantelte Ablenkung von Silberatomen in einem inhomogenen Magnetfeld.
Spin
In der Quantenmechanik wird der „Eigendrehimpuls“ eines Quantenobjekts als Spin bezeichnet. Der Spin ist allerdings eine abstrakte Größe ohne anschauliche Bedeutung, die nur in Form bestimmter ganzzahliger (Bosonen) oder halbzahliger (Fermionen) Vielfacher des Planckschen Wirkungsquantums in Erscheinung tritt (). Elementarteilchen mit mit den Spins werden zwar postuliert, konnten aber bislang nicht nachgewiesen werden.
Siehe auch
- Drehimpuls - Artikel in der deutschen Wikipedia
- Spin - Artikel in der deutschen Wikipedia
































