Eine freie Initiative von Menschen bei mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| Use Google Translate for a raw translation of our pages into more than 100 languages. Please note that some mistranslations can occur due to machine translation. |
Neuronales Netz
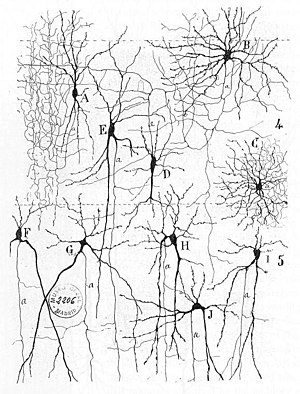
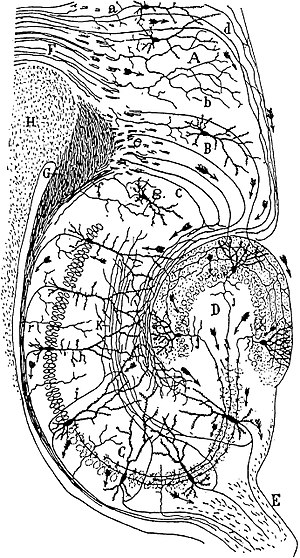


mit Divergenz: ein Neuron gibt Signale an mehrere andere Neuronen weiter,
und Konvergenz: ein Neuron erhält Signale von mehreren anderen.
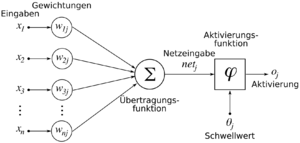
Ein neuronales Netz besteht aus einer Vielzahl in funktionellen hierarchischen Ebenen angeordneter, miteinander über Synapsen vernetzter Neuronen (Nervenzellen), die auf der feinsten Ebene des Nervensystems, der Mikoskala, einen funktionellen Zusammenhang bilden. Auf der Mesoskala ist die Großhirnrinde darüber hinaus in kortikalen Säulen mit einem durchschnittlichen Durchmesser von etwa 80 Mikrometern organisiert, die aus einigen hundert oder tausend Neuronen bestehen. Die Makroskala wird durch die weitreichenden Verbindungen zwischen den verschiedenen spezialisierten Hirnarealen gebildet. Die Gesamtheit all dieser vielfältigen Nervenverbindungen wird als Konnektom bezeichnet.
Grundlagen
Eine erste Darstellung[1] gab 1894 der österreichischer Physiologe Sigmund Exner in seinem Entwurf zu einer physiologischen Erklärung der psychischen Erscheinungen[2]. Üblicherweise verfügen neuronale Netze über eine Vielzahl von Eingängen und einen einzigen Ausgang. Durch ihre hohe funktionelle und strukturelle neuronale Plastizität, durch die die synaptischen Verbindungen der Nervenzellen aktivitätsabhängig beständig umgebildet und neu gewichtet werden, sind neuronale Netze hochgradig lernfähig. Daneben findet zwischen Neuronen und Zellen der Neuroglia, insbesondere mit den Oligodendrozyten und Astrozyten, ein chemischer und elektrischer Austausch statt, der die Gewichtung der Signale verändern kann. Neuronale Netze folgen dadurch nicht explizit vorgegebenen Regeln, sondern entwickeln bei entsprechendem Training durch implizites Lernen eine eigenständige Art von neuronaler Intelligenz. Hervorstechend ist insbesondere ihre Fähigkeit, komplexe Muster zu erkennen und zu speichern.
Die Struktur der neuronalen Netze und der Bau des Gehirns insgesamt ist in gewissem Sinn eine physisch realisierte Imagination der geistig-seelischen Tätigkeit des Menschen. Darauf hat schon Rudolf Steiner hingewiesen:
„Ich war einmal in einer Versammlung — es ist schon viele Jahre her —, da sprach zuerst ein Arzt über den Gehirnbau, setzte den Gehirnbau auseinander im Zusammenhang mit dem Seelenleben des Menschen, nach einer Anschauung, die man ganz mit Recht materialistisch nennen kann. Es war ein ganz waschechter Materialist, der da den Gehirnbau ganz gut auseinandersetzte, soweit er heute durchforscht ist, und der also das Seelenleben im Zusammenhang mit diesem Gehirnbau erklärte. Der Vorsitzende dieser Versammlung war ein Herbartianer, und der konstruierte sich nun nicht den Gehirnbau, aber dasjenige, was das Vorstellungsleben ist, so wie es der Philosoph Herhart einmal gemacht hat. Der sagte dann: Ja, es ist doch merkwürdig, der Physiologe, der Arzt, der zeichnet das Gehirn auf und macht da Figuren; wenn ich als Herbartianer, sagte er, die komplizierten Vorstellungsassoziationen aufzeichne, wobei ich bloß ein Bild meine von dem, was sich als Vorstellungen vergesellschaftet, nicht etwa Nervenfäden, die eine Nervenzelle mit der anderen verbinden, wenn ich als richtiger Herbartianer, der sich nicht um das Gehirn kümmert, dasjenige, was ich mir vorstelle über die Art, wie sich Vorstellungen verketten und so weiter, nur ganz symbolisch zeichne, so sieht das ganz ähnlich aus wie die Zeichnungen des Physiologen über den physischen Gehirnbau.
Das ist nicht ohne Grund, daß das ähnlich ausschaut. Indem wir immer mehr und mehr auf den Bau des Gehirnes naturwissenschaftlich gekommen sind, hat sich nämlich immer mehr und mehr gezeigt, daß eigentlich der äußere Bau des Gehirnes in einer ganz wunderbaren Weise dem Bau unseres Vorstellungslebens entspricht. Man kann alles, was man im Vorstellungsleben findet, im Gehirnbau wiederfinden. Es ist einfach — bitte nehmen Sie das cum grano salis —, wie wenn die Natur selber im Gehirn ein plastisches Abbild unseres Vorstellungslebens hätte schaffen wollen. So etwas fällt einem ganz besonders auf, wenn man, sagen wir, solche Darstellungen wie die von Meynert liest. Jetzt sind sie schon etwas veraltet. Meynert ist Materialist gewesen, aber ausgezeichneter Gehirnphysiologe, Psychiater, und man möchte sagen: Ja, der ist Materialist, aber dasjenige, was er einem als Materialist gibt, das ist eine wunderbare Abschlagszahlung für dasjenige, was man auch herauskriegt, auch wenn man sich gar nicht kümmert um das menschliche Gehirn, sondern bloß darum, wie sich Vorstellungen verknüpfen und trennen und so weiter und bloß diese Symbole hinzeichnen will. — Kurz, es ist so, daß man, wenn man durch irgend etwas Materialist werden könnte, man es durch den Bau des menschlichen Gehirnes ganz besonders werden könnte. Jedenfalls muß man sagen, wenn es ein Geistig-Seelisches gibt, so hat dieses Geistig-Seelische im menschlichen Gehirn einen so adäquaten Ausdruck gefunden, daß man nun gar nicht weit von der Behauptung ist: Ja, was braucht man noch ein Geistig-Seelisches für das Vorstellungsleben? Wenn man noch eine Seele verlangen würde, die noch denken kann! Da das Gehirn eine so genaue Abbildung ist des Geistig-Seelischen, warum soll das Gehirn nicht denken können? -
Alle diese Dinge müssen Sie natürlich mit dem bekannten Gran Salz verstehen. Ich will nur auf den Sinn der ganzen Auseinandersetzung heute hinweisen. Das menschliche Gehirn kann einen schon, besonders wenn man in die Detailforschung eingeht, zum Materialisten machen. Und was da so eigentlich für ein Geheimnis obwaltet, was da eigentlich zugrunde liegt, das wird einem doch erst klar, wenn man zur imaginativen Erkenntnis kommt. In der imaginativen Erkenntnis nämlich zeigen sich einem Bilder, Bilder für nur wirklich Geistiges, Bilder, die man früher nicht gesehen hat. Aber man möchte sagen, diese Bilder erinnern einen an die durch die Nervenzellen und Nervenfäden geformten Bilder im menschlichen Gehirn. Und ich möchte sagen, wenn ich Ihnen eine Erklärung geben sollte für die Frage: Was ist eigentlich dieses imaginative Erkennen, das natürlich ganz im Übersinnlichen verläuft, was ist es? Wenn ich Ihnen gleichsam versinnbildlichen sollte die imaginative Erkenntnis, wie der Mathematiker es mit seinen Figuren macht, indem er mathematische Probleme aufzeichnet, dann könnte ich auch sagen: Man stelle sich vor, daß man in der Welt mehr erkennt, als was die Sinneserkenntnis gibt, dadurch, daß man aufsteigen kann zu Bildern, die eine Realität so geben, wie das menschliche Gehirn die menschliche Seelenrealität gibt. Die Natur selber stellt das hin als eine reale, als eine sinnlichreale Imagination im Gehirn, was man eigentlich in der imaginativen Erkenntnis auf einem höheren Gebiete erlangt.
Aber dadurch kommt man tiefer jetzt hinein in die menschliche Konstitution. Wir werden das in den nächsten Tagen sehen: Man kommt immer zu einer Möglichkeit, diesen Wunderbau des menschlichen Gehirns nicht isoliert für sich zu sehen, sondern ich möchte sagen: Während man eine Welt, eine übersinnliche Welt oben durch Imagination sieht, ist es so, wie wenn ein Teil dieser Welt sich herunterrealisiert hätte und im menschlichen Gehirn eine realisierte imaginative Welt vor uns dastehen würde. Und in der Tat, ich glaube nicht, daß irgend jemand adäquat über das menschliche Gehirn sprechen kann, der nicht in dem menschlichen Gehirnbau eine imaginative Darstellung des Seelenlebens sieht. Das ist auch dasjenige, was uns immer wiederum in eine Zwickmühle führt, wenn wir von der bloßen Gehirnphysiologie ausgehen und zum Seelenleben hinüberkommen wollen. Nämlich, wenn man beim Gehirn stehenbleiben will, braucht man gar nicht das Seelenleben. Nur derjenige hat ein Recht, gegenüber dem Bau des menschlichen Gehirnes noch von einem Seelenleben zu sprechen, der dieses Seelenleben außerdem noch anders kennt, als man es kennt auf dem gewöhnlichen Wege dieser Welt. Denn wenn man in der geistigen Welt dieses Seelenleben kennenlernt: im Bau des menschlichen Gehirnes hat es sein adäquates Abbild, und alles das, was das übersinnliche Seelenorgan vorstellungsgemäß kann, kann das Gehirn auch. Denn bis in die Funktionen hinein ist das Gehirn ein Abbild; so daß niemand Materialismus belegen oder widerlegen kann von der Gehirnphysiologie aus. Das gibt es einfach nicht. Wenn der Mensch bloß Gehirnwesen wäre, so würde man gar nicht daraufzukommen brauchen, daß er noch eine Seele hat.“ (Lit.: GA 314, S. 88ff)
Rekurrente neuronale Netze
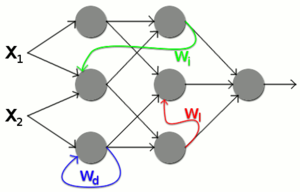
Bei rückgekoppelten bzw, rekurrenten neuronalen Netzen, wie sie vor allem im Neocortex vorkommen, sind die Neuronen einer Rindenschicht entweder mit Neuronen derselben oder einer darunterliegenden Schicht rückgekoppelt. Dabei gibt es verschiedene Verschaltungsmöglichkeiten:
- direkte Rückkopplung (eng. direct feedback): der Ausgang wird als Eingang auf dasselbe Neuron zurückgeführt ()
- indirekte Rückkopplung (eng. indirect feedback: der Ausgang wird an ein Neuron einer darunterliegenden Schicht weitergeleitet ()
- laterale Rückkopplung (eng. eng. lateral feedback: der Ausgang des Neurons wird seitlich an ein anderes Neuron derselben Schicht weitergeleitet ()
- vollständige Rückkopplung: jeder Ausgang des Neurons ist mit einem anderen Neuron verbunden
Künstliche neuronale Netze

Der technische Nachbau neuronaler Netze durch künstliche neuronale Netze (kurz: KNN; eng. artificial neural network, ANN) ist für die Entwicklung der künstlichen Intelligenz von hervorragender Bedeutung. Die Grundlage dafür bietet das softwaremäßig, seltener auch hardwaremäßig realisierte Modell eines künstlichen Neurons.
Ein einfaches Modell eines künstlichen Neurons wurde erstmals 1943 von Warren McCulloch und Walter Pitts in Form der nach ihnen benannten McCulloch-Pitts-Zelle vorgeschlagen[3], mit der sich einfache logische AND-, OR- und NOT-Gatter simulieren lassen, mit denen mathematische und logische Operationen durchgeführt werden können. Sie wollten damit die Frage klären, ob das Gehirn Turing-berechenbare Funktionen berechnen kann und die Gehirntätigkeit damit im Prinzip auf Rechenoperationen rückführbar ist. Diese Idee hatte erstmals schon der englische Mathematiker und Philosoph Thomas Hobbes (1588-1679) vorgeschlagen:
„Unter rationeller Erkenntnis vielmehr verstehe ich Berechnung. Berechnen heißt entweder die Summe von zusammengefügten Dingen finden oder den Rest erkennen, wenn eins vom andern abgezogen wird. Also ist rationelle Erkenntnis dasselbe wie Addieren und Subtrahieren; wenn jemand Multiplizieren, und Dividieren hinzufügen will, so habe ich nichts dagegen, da Multiplikation dasselbe ist wie Addition gleicher Posten, Division dasselbe wie eine bestimmte Subtraktion gleicher Posten. Aber rationelle Erkenntnis geht jedenfalls auf zwei Geistesoperationen zurück: Addition und Subtraktion.“
Künstliche rekurrente neuronale Netze
Künstliche rekurrente neuronale Netze (RNNs) sind eine Art von künstlichen neuronalen Netzen, die speziell für die Verarbeitung von sequenziellen Daten wie Sprache, Zeitreihen oder Musik entwickelt wurden. Im Gegensatz zu traditionellen neuronalen Netzen haben RNNs eine Art von Gedächtnis, das es ihnen ermöglicht, vergangene Informationen beizubehalten und sie bei der Verarbeitung neuer Eingaben zu berücksichtigen. Auch der Neocortex, beruht vorwiegend auf rekurrenten neuronalen Netzen (siehe oben).
Ein RNN besteht aus einer Schleife von Neuronen, die Informationen von einem Zeitschritt zum nächsten weitergeben und dabei einen internen Zustand (den sogenannten "hidden state") aktualisieren. Der aktuelle Zustand hängt sowohl von der aktuellen Eingabe als auch vom vorherigen Zustand ab, so dass das Netzwerk eine Art von Kontext beibehält und somit Informationen aus der Vergangenheit berücksichtigt.
RNNs können in verschiedenen Architekturen konstruiert werden, z.B. als einfache RNNs, die nur eine Schleife von Neuronen haben, oder als komplexere Modelle wie LSTM (Long Short-Term Memory) oder GRU (Gated Recurrent Unit), die speziell zur Verarbeitung von langfristigen Abhängigkeiten entwickelt wurden.
RNNs werden in vielen Anwendungen eingesetzt, wie z.B. Spracherkennung, maschinelles Übersetzen, Textgenerierung, Vorhersage von Zeitreihen und Musikkomposition.
Hebbsche Lernregel
1949 formulierte der kanadische Kognitionspsychologe Donald O. Hebb (1904-1985) in seinem Buch The Organization of Behavior die mittlerweile experimentell gut belegte grundlegende und einfachste neuronale Lernregel, die sog. Hebbsche Lernregel, die kurz gefasst besagt: „what fires together, wires together“, d.h. je öfter Neuronen gleichzeitig feuern, umso bevorzugter werden sie auch künftig durch Ausbildung entsprechender synaptischer Verbindungen miteinander aktiv werden. Dies konnte Hebb durch die Veränderungen der synaptischen Übertragung zwischen den Neuronen nachweisen. Als endgültige Bestätigung gelten die Experimente von Terje Lømo und anderen in den 1960er und 1970er Jahren[4] und der direkte Nachweis der Veränderung von Signalübertragung als Teil des Mechanismus für Lernprozesse und Gedächtnis im Jahr 2014.[5] Hebb gilt damit als der Entdecker des Modells der synaptischen Plastizität, welche die neurophysiologische Grundlage von Lernen und Gedächtnis darstellt.[6]
In künstlichen neuronalen Netzen wird die Hebbsche Lernregel durch die Gewichtsänderung des neuronalen Graphen abgebildet. Sie ist proportional zu der als passende Konstante gewählten Lernrate und zur Aktivitätsrate des Neuronsi und dem Output des mit ihm verbundenen Neuronsj, d.h.
Siehe auch
- Neuronales Netz - Artikel in der deutschen Wikipedia
- Künstliches neuronales Netz - Artikel in der deutschen Wikipedia
- Hebbsche Lernregel - Artikel in der deutschen Wikipedia
- Neuronale Plastizität - Artikel in der deutschen Wikipedia
Literatur
- Thomas Hobbes: Grundzüge der Philosophie: Vom Körper / Vom Menschen / Vom Bürger, übersetzt von Max Frischeisen-Köhler. Hofenberg Verlag 2017, ISBN 978-3743722026, eBook Jazzybee Verlag 2012 ASIN B00B4ON904
- Donald Olding Hebb: The organization of behavior. A neuropsychological theory. Erlbaum Books, Mahwah, N.J. 2002, ISBN 0-8058-4300-0
- Manfred Spitzer: Geist im Netz. Spektrum Akademischer Verlag, Heidelberg 1996, ISBN 3-8274-0109-7, S. 148–182
- Norman Doidge, Jürgen Neubauer (Übers.): Neustart im Kopf: wie sich unser Gehirn selbst repariert. Campus-Verlag, Frankfurt am Main / New York 2008, ISBN 978-3-593-38534-1
- Rudolf Steiner: Physiologisch-Therapeutisches auf Grundlage der Geisteswissenschaft. Zur Therapie und Hygiene, GA 314 (1989), ISBN 3-7274-3141-5 pdf pdf(2) html mobi epub archive.org English: rsarchive.org
 Literaturangaben zum Werk Rudolf Steiners folgen, wenn nicht anders angegeben, der Rudolf Steiner Gesamtausgabe (GA), Rudolf Steiner Verlag, Dornach/Schweiz Email: verlag@steinerverlag.com URL: www.steinerverlag.com.
Freie Werkausgaben gibt es auf steiner.wiki, bdn-steiner.ru, archive.org und im Rudolf Steiner Online Archiv. Eine textkritische Ausgabe grundlegender Schriften Rudolf Steiners bietet die Kritische Ausgabe (SKA) (Hrsg. Christian Clement): steinerkritischeausgabe.com Die Rudolf Steiner Ausgaben basieren auf Klartextnachschriften, die dem gesprochenen Wort Rudolf Steiners so nah wie möglich kommen. Hilfreiche Werkzeuge zur Orientierung in Steiners Gesamtwerk sind Christian Karls kostenlos online verfügbares Handbuch zum Werk Rudolf Steiners und Urs Schwendeners Nachschlagewerk Anthroposophie unter weitestgehender Verwendung des Originalwortlautes Rudolf Steiners. |
Weblinks
- Einführung in die Grundlagen und Anwendungen neuronaler Netze
- Einführung in Neuronale Netze (Memento vom 15. Mai 2001 im Internet Archive)
- Geschichte der Neuronalen Netze bis 1960 (Memento vom 3. Februar 2006 im Internet Archive) (engl.)
- Ein kleiner Überblick über Neuronale Netze (D. Kriesel) - Ausführliche, illustrierte Arbeit zu Neuronalen Netzen; Themen sind u. a. Perceptrons, Backpropagation, Radiale Basisfunktionen, Rückgekoppelte Netze, Self Organizing Maps, Hopfield-Netze.
- Neuronale Plastizität: Das formbare Gehirn (PDF) In: Forschungsperspektiven 2010+, Max-Planck-Gesellschaft.
- Ulrich Kraft: Altern mit Köpfchen. (PDF; 2,6 MB) In: MaxPlanckForschung, Heft 1/2007
- Models of Synaptic Plasticity. In: Scholarpedia. (englisch, inkl. Literaturangaben)
- Harel Z. Shouval: Maintenance of synaptic plasticity. In: Scholarpedia. (englisch, inkl. Literaturangaben)
Einzelnachweise
- ↑ Olaf Breidbach: Hirn, Hirnforschung. In: Werner E. Gerabek, Bernhard D. Haage, Gundolf Keil, Wolfgang Wegner (Hrsg.): Enzyklopädie Medizingeschichte. De Gruyter, Berlin/New York 2005, ISBN 3-11-015714-4, S. 600 f.; hier: S. 600 (und S. 1543).
- ↑ Sigmund Exner: Entwurf zu einer physiologischen Erklärung der psychischen Erscheinungen von Dr. Sigmund Exner: I. Theil, F. Deuticke, Leipzig Wien 1894
- ↑ Warren McCulloch, Walter Pitts: A logical calculus of the ideas immanent in nervous activity. In: Bulletin of Mathematical Biophysics, Bd. 5 (1943), S. 115–133, ISSN 0007-4985 pdf
- ↑ T. V. Bliss, T. Lomo: Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. In: J Physiol. 232(2), 1973, S. 331–356, Free Full Text Online. PMID 4727084
- ↑ G. Yang, C. S. Lai, J. Cichon, L. Ma, W. Li, W. B. Gan: Sleep promotes branch-specific formation of dendritic spines after learning. In: Science. 344(6188), 2014, S. 1173–1178. PMID 24904169
- ↑ Manfred Spitzer: Geist im Netz, Modelle für Lernen, Denken und Handeln. Spektrum Akademischer Verlag, Heidelberg 1996, ISBN 3-8274-0109-7, S. 107.




















