Eine freie Initiative von Menschen bei mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| Use Google Translate for a raw translation of our pages into more than 100 languages. Please note that some mistranslations can occur due to machine translation. |
Atomorbital

Atomorbitale beschreiben die Energie und Aufenthaltswahrscheinlichkeit der Elektronen in der Elektronenhülle eines Atoms. Experimentell kann die Verteilung der Elektronendichte bei kristallisierbaren Materialien bis zu einem gewissen Grad mittels Röntgenstrukturanalyse bestimmt werden.
Quantenmechanische Beschreibung der Atomorbitale
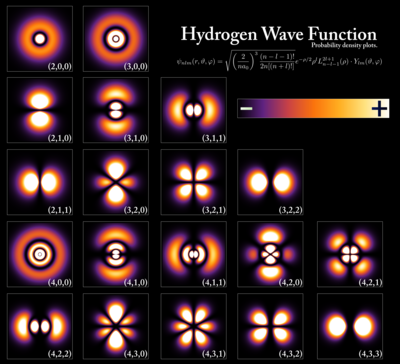
Entsprechend der Quantenhypothese unterliegen Elektronen dem Welle-Teilchen-Dualismus und können daher weder als genau lokalisierbare materielle Teilchen aufgefasst werden, noch kann ihnen eine definierte Bahn um den Atomkern zugeschrieben werden. Vielmehr halten sie sich nur mit einer quantenmechanisch berechenbaren Aufenthaltswahrscheinlichkeit in bestimmten räumlichen Bereichen auf, eben den Atomorbitalen, deren Form und Ausdehnung durch verschiedene Quantenzahlen bestimmt ist. Quantenmechanisch betrachtet handelt es sich bei den Atomorbitalen um Wellenfunktionen , die sich als Lösungen der Schrödingergleichung ergeben.
Darin bedeutet die imaginäre Einheit, die vom Ort und der Zeit abhängige komplexe Wellenfunktion, das reduzierte Plancksche Wirkungsquantum und den Hamiltonoperator (Energieoperator) des betrachteten Systems.
Da es sich bei der Beschreibung der Elektronenhülle um ein stationäres System handelt, ist der folgende Lösungsansatz naheliegend:
Die Zeitabhängigkeit wird hier durch den periodischen Faktor mit der konstanten Frequenz ausgedrückt. Für den zeitunabhängigen Faktor ergibt sich daraus die Eigenwertgleichung, aus der sich die Energie der Orbitale berechnen lässt:
Bornsche Wahrscheinlichkeitsinterpretation
Nach der 1926 von Max Born (1882-1970) vorgeschlagenen statistischen Deutung der Quantenmechanik entspricht das Betragsquadrat der Wellenfunktion der Aufenthaltswahrscheinlichkeitsdichte des Teilchens. Dazu muss die Wellenfunktion allerdings so normiert werden, dass die Gesamtwahrscheinlichkeit = 1 ist:
Quantenzahlen
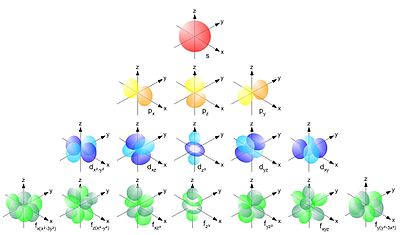
Die Elektronenkonfiguration der Elektronenhülle wird durch vier Quantenzahlen bestimmt:
- Die Hauptquantenzahl beschreibt das Hauptenergieniveau bzw. die sog. Schale, in der sich das Elektron aufhält.
- Die Nebenquantenzahl oder Drehimpulsquantenzahl charakterisiert die Symmetrie der sog. Atomorbitale, in denen sich die Elektronen aufhalten. Da es sich bei der Elektronenbewegung im Prinzip um Schwingungsvorgänge bzw. um stehende Wellen handelt, die mathematisch durch die Schrödingergleichung beschrieben werden, ähneln sie nicht zufällig den Chladnischen Klangfiguren. Die Unterschalen werden dabei üblicherweise mit folgenden Buchstaben bezeichnet, die historisch aus der Spektroskopie übernommen wurden:
- s für (ursprünglich für ‚scharf‘, z. B. „s-Zustand“) - kugelsymmetrische (s-Schale)
- p für (ursprünglich für engl. ‚principal‘, ‚Haupt‘-Zustand) - hantelförmig (p-Schale)
- d für (ursprünglich für ‚diffus‘) - gekreuzte Doppelhantel (d-Schale)
- f für (ursprünglich für ‚fundamental‘) - rosettenförmig (f-Schale)
- g für (alphabetische Fortsetzung) - rosettenförmig (g-Schale)
- h für (alphabetische Fortsetzung) - rosettenförmig (h-Schale)
- Die magnetische Quantenzahl oder Richtungsquantenzahl bestimmt die räumliche Orientierung der Orbitale. Entsprechend der magnetischen Quantenzahl gibt es je Unterschale 1 s-Orbital, 3 p-Orbitale, 5 d-Orbitale, 7 f-Orbitale, 9 g-Orbitale und 11 h-Orbitale, von denen jedes nach dem Pauli-Prinzip (siehe unten) zwei durch ihre Spinrichtung unterscheidbare Elektronen aufnehmen kann. Die Orbitale mit gleicher Haupt- und Nebenquantenzahl liegen trotz unterschiedlicher magnetischer Quantenzahlen auf dem gleichen Energieniveau und werden als entartet bezeichnet. Sie werden nur in einem starken magnetischen (Zeeman-Effekt) oder elektrischen Feld (Stark-Effekt) aufgespalten.
- Die Spinquantenzahl kann für Elektronen nur die Werte und annehmen und charakterisiert den abstrakt-formalen Eigendrehimpuls, den Spin, des Elektrons.
Die Konfiguration der äußersten Elektronenschale, der sogenannten Valenzschale, welche die Valenzelektronen (auch: Außenelektronen) enthält, bestimmt die chemischen Eigenschaften und den Platz im Periodensystem der chemischen Elemente.
Pauli-Prinzip
Nach dem 1925 von Wolfgang Pauli formulierten und für alle Fermionen gültigen Pauli-Prinzip (auch Pauli-Verbot oder Paulisches Ausschließungsprinzip) dürfen dabei die Elektronen der Hülle nicht in allen Quantenzahlen übereinstimmen. Jedes Atomorbital kann daher von maximal zwei Elektronen besetzt werden, die sich durch ihren Spin unterscheiden. Die Elektronen können sich daher nicht im untersten, energieärmsten Atomorbital zusammendrängen, sondern müssen sich auch auf höhere, ausgedehntere und energiereichere Orbitale verteilen und bedingen dadurch die relativ große Ausdehnung der Elektronenhülle, die oben schon durch die Heisenbergsche Unbestimmtheitsrelation gerechtfertigt wurde. Das Pauli-Prinzip folgt aus der Tatsache, dass die Elektronen - wie alle gleichartigen Quantenobjekte - prinzipiell ununterscheidbar sind, was nochmals verdeutlicht, dass Elektronen nicht als materielle, sondern als ideelle „Objekte“, also als Ideen aufzufassen sind, die das Auftreten bestimmter messbarer Eigenschaften („Observablen“) wie z.B. der elektrischen Ladungsdichte gesetzmäßig regeln.
Aufbauprinzip

Das Aufbauprinzip der Elektronenhülle beruht darauf, dass die Atomorbitale schrittweise in Richtung zunehmender Energie aufgefüllt werden. Die Energieniveaus folgen dabei der empirisch gefundenen -Regel (Madelung-Regel), wonach Orbitale mit kleinerem -Wert energetisch tiefer liegen. Bei gleichen Werten ist ist das Orbibtal mit kleinerem begünstigt. Daraus ergibt sich folgende Besetzungsreihenfolge, von der es nur ganz seltene Ausnahmen gibt (Lanthan, Kupfer, Chrom):
Entartete Energieniveaus (z.B. die px-, py- und pz-Orbitale) werden nach der Hundschen Regel zuerst mit je einem Elektron mit parallelem Spin besetzt, womit eine größtmögliche räumliche Verteilung der Elektronen und ein maximaler Gesamtspin erzielt wird.[1]
Periodensystem
Aus dem Aufbauprinzip ergibt sich unmittelbar die Ordnung des Periodensystems, insbesondere auch die Unterscheidung von Haupt- und Nebengruppen. Die Elemente der Nebengruppen, die Übergangsmetalle, verfügen nach der Besetzungsregel über nur unvollständig aufgefüllte d-Schalen (ausgenommen die Zink-Gruppe), da zuerst die nächsthöhere s-Schale besetzt wird.

Hybridorbitale

Um die geometrischen Verhältnisse von Molekülen wirklichkeitsgetreuer zu beschreiben, führte Linus Pauling um 1931 das Konzept der Hybridorbitale ein. Er nützte dabei die Tatsache aus, dass alle Linearkombinationen der Wellenfunktionen, die sich als Lösungen der Schrödingergleichung ergeben, gültige Lösungen derselben sind.
Ein Beispiel möge dies verdeutlichen: Ein Kohlenstoffatom (C) verbindet sich mit vier Wasserstoffatomen (H) zu dem Kohlenwasserstoff Methan (CH4). Wasserstoff verfügt nur über ein einziges Elektron, das sich im Grundzustand im 1s-Orbital aufhält. Kohlenstoff hat insgesamt 6 Elektronen, von denen sich zwei in der inneren 1s-Schale befinden, die an der Bindung unbeteiligt ist. Die restlichen 4 Elektronen befinden sich in der 2. Schale und verteilen sich auf das kugelsymmetrische 2s-Orbital und die drei hantelförmigen 2p-Orbitale, d.h. auf 2px, 2py und 2pz, die rechtwinkelig zueinander stehen. Da die kovalente Bindung der 4 Wasserstoffatome an den Kohlenstoff durch Überlagerung der äußeren Atomorbitale erfolgt, müssten theoretisch unterschiedliche Bindungen entstehen je nach dem, ob sich das 1s-Orbital des Wasserstoffs mit dem 2s-Orbital oder einem der drei 2p-Orbitale des Kohlenstoffs überlagert. Empirisch zeigt sich allerdings, dass alle 4 Bindungen völlig gleichwertig und nach den Ecken eines Tetraeders ausgerichtet sind. Das Problem lässt sich lösen, wenn man das 2s-Orbital und die drei 2p-Orbitale durch Linearkombination zu vier gleichwertigen sp3-Hybridorbitalen umwandelt, die tetraedrisch ausgerichtet und mit je einem Elektron besetzt sind.
Literatur
- Viktor Gutmann, Edwin Hengge: Allgemeine und anorganische Chemie, 5. Auflage, Verlag Chemie, Weinheim 1990, ISBN 978-3527281596
- A. F. Holleman, E. Wiberg, N. Wiberg: Lehrbuch der Anorganischen Chemie, 102. Auflage, de Gruyter, Berlin 2007, ISBN 978-3-11-017770-1
- K. P. C. Vollhardt, Neil E. Schore, Holger Butenschön (Hrsg.): Organische Chemie, 5. Auflage, Wiley-VCH 2011, ISBN 978-3527327546
- Paula Y. Bruice: Organische Chemie: Studieren kompakt, 5. Auflage, Pearson Studium 2011, ISBN 978-3868941029, eBook ASIN B00QV6QM0O
Einzelnachweise
- ↑ Eric R. Scerri: How Good Is the Quantum Mechanical Explanation of the Periodic System?, in: Journal of Chemical Education. 75, Nr. 11, 1998, S. 1384–85. doi:10.1021/ed075p1384 pdf
| Dieser Artikel basiert auf einer für AnthroWiki adaptierten Fassung des Artikels Atomorbital aus der freien Enzyklopädie de.wikipedia.org und steht unter der Lizenz Creative Commons Attribution/Share Alike. In Wikipedia ist eine Liste der Autoren verfügbar. |









































