Eine freie Initiative von Menschen bei mit online Lesekreisen, Übungsgruppen, Vorträgen ... |
| Use Google Translate for a raw translation of our pages into more than 100 languages. Please note that some mistranslations can occur due to machine translation. |
Welle

|
| |
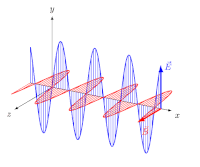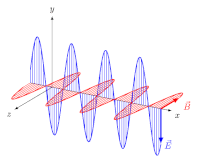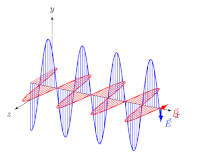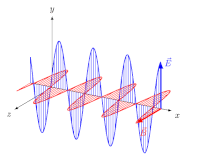
Linear polarisierte elektromagnetische Welle im Vakuum. Die monochromatische Welle mit der Wellenlänge breitet sich in x-Richtung aus, die elektrische Feldstärke (in blau) und die magnetische Flussdichte (in rot) stehen zueinander und zur Ausbreitungsrichtung im rechten Winkel.
| ||
Eine Welle ist aus physikalischer Sicht eine sich räumlich mit einer bestimmten Geschwindigkeit ausbreitende Veränderung (Störung) bzw. Schwingung einer orts- und zeitabhängigen physikalischen Größe. Dabei wird keine Materie, wohl aber Energie transportiert. Mechanische Wellen - wie beispielsweise Schallwellen oder Wasserwellen - bedürfen für ihre Ausbreitung eines materiellen Trägers (bei Schallwellen z.B. Luft, Wasser oder auch Festkörper), während sich etwa elektromagnetische Wellen auch im Vakuum ausbreiten können.
Grundlagen
Fällt die Schwingungsrichtung mit der Ausbreitungsrichtung zusammen, spricht man von Logitudinalwellen, während bei Transversalwellen die Schwingung quer zur Ausbreitungsrichtung erfolgt. Dreht sich dabei die Schwingungsebene um die Ausbreitungsachse, spricht man von Torsionswellen. Schallwellen breiten sich in Flüssigkeiten und Gasen als Longitudinalwellen aus, in Festkörpern hingegen ähnlich den elektromagnetischen Wellen auch als Transversalwellen.



Bei Transversalwellen kann das Phänomen der Polarisation auftreten. Bei konstanter Schwingungsrichtung handelt es sich um eine lineare Polarisation. Bei der zirkularen Polarisation (früher auch drehende Polarisation genannt) ändert sich die Schwingungsrichtung hingegen mit konstanter Winkelgeschwindigkeit. Eine Mischform dieser beiden Möglichkeiten ist die elliptische Polarisation. Ändert sich die Schwingungsrichtung beständig und völlig ungeordnet, ist die Welle unpolarisiert.
Die Wellenlänge ist der kleinste Abstand zweier Punkte in gleicher Phase und umgekehrt proportional zur Frequenz , mit der Phasengeschwindigkeit als Proportionalitätsfaktor. Ihr Kehrwert ist die Wellenzahl , die die Anzahl der Wellenlängen pro Längeneinheit angibt. Für monochromatische Wellen ist die Ausbreitungsgeschwindigkeit der Welle mit der Phasengeschwindigkeit identisch.
- bzw.
Für elektromagnetische Wellen ist die Phasengeschwindigkeit gleich der Lichtgeschwindigkeit, d.h. der endliche Ausbreitungsgeschwindigkeit des Lichts im Vakuum. Nach den Maxwellschen Gleichungen der Elektrodynamik ist sie unabhängig von der Frequenz und der Bewegung der Lichtquelle stets konstant. Ihr Wert beträgt . Aus der Konstanz der Vakuumlichtgeschwindigkeit folgen die 1905 von Albert Einstein veröffentlichten Gesetzmäßigkeiten der speziellen Relativitätstheorie.
Die Wellenfront ist eine ebene oder gekrümmte Fläche, auf der alle Punkte mit gleicher Laufzeit vom Sender liegen. Senkrecht auf die Wellenfront steht der Wellenvektor oder Wellenzahlvektor . Der Betrag des Wellenvektors ist die Kreiswellenzahl : die Bezeichnung Wellenzahlvektor:
Sinuswelle





Eine monochromatische Welle, d.h. eine Welle mit nur einer einzigen Frequenz, kann als harmonische Welle, d.h. als Sinuswelle durch die Funktion beschrieben werden. ist dabei die Amplitude, die Kreisfrequenz, die Zeit und die Anfangsphase der Welle.
Stehende Welle und Wanderwelle
Eine stehende Welle ist dadurch gekennzeichnet, dass ihre Auslenkung - im Gegensatz zu einer fortschreitenden Wanderwelle - an bestimmten Stellen, den Wellenknoten, stets Null bleibt, während sie an anderen, den Wellenbäuchen, weit ausschwingt.
Wellenpaket
Ein Wellenpaket ist eine räumlich oder zeitlich begrenzte Welle. Mathematisch kann sie durch Überlagerung (Superposition) mehrerer harmonischer Wellen (Sinuswellen) erzeugt werden (→ Fourier-Synthese) bzw. durch Fourier-Analyse bzw. experimentell durch Spektralanalyse wieder in ihre Bestandteile zerlegt werden.
Ist die Phasengeschwindigkeit der Welle von der Frequenz abhängig, kommt es zur Dispersion durch die das Wellenpaket mit fortschreitender Zeit zerfließt. Die Geschwindigkeit, mit der sich die Einhüllende eines Wellenpakets bewegt, ist die Gruppengeschwindigkeit. Im Allgemeinen, insbesondere wenn die Phasengeschwindigkeit stark frequenzabhängig ist oder die Absorption nicht vernachlässigt werden kann, ist die Signalgeschwindigkeit von der Gruppengeschwindigkeit zu unterscheiden. Die Geschwindigkeit mit der sich die erste Auslenkung einer Wellenfront bewegt, also die Frontgeschwindigkeit - und damit auch die Signalgeschwindigkeit - ist immer kleiner als die Lichtgeschwindigkeit.
Ebene Welle
Eine ebene Welle breitet sich so im dreidimensionalen Raum aus, dass ihre Wellenfronten, d.h. die Flächen mit gleichen Phasenwinkel, senkrecht zur Ausbreitungsrichtung stehen.
Wellengleichung
Mathematisch betrachtet ist eine Welle im -dimensionalen Raum eine Lösung der allgemeinen Wellengleichung.
Für die homogene Wellengleichung gilt:
- bzw. mit dem Laplace-Operator bzw. kurz
mit dem d’Alembert-Operator (Box)
Mit der Inhomogenität oder Quelle von ergibt sich entsprechend für die inhomogene Wellengleichung:
Für eine eindimensionalen homogene Welle folgt daraus die vereinfachte Form:
Mittels Fourier-Transformation lässt sich die allgemeine Lösung der Wellengleichung mit der Kreisfrequenz als Linearkombination komplexer Exponentialfunktionen bzw. Sinusfunktionen folgender Form darstellen:
- bzw.
Siehe auch
Literatur
- Christian Gerthsen, Dieter Meschede: Gerthsen Physik. 25. Auflage. Springer Spektrum 2015, ISBN 978-3662459768; eBook ASIN B015SSB1AG
- Douglas C. Giancoli: Physik. 4. Auflage. Pearson Studium 2019. ISBN 978-3868943634; eBook ASIN B07W8LVB6L














































